A block of mass m is pl aced on a smooth wedge of inclination $θ$ . The whole system is accelerated horizontally so that the block does not slip on the wedge. Find the
(i) Acceleration of the wedge
(ii) Force to be applied on the wedge
(iii) Force exerted by the wedge on the block.

Text Solution

Verified by Experts

(I) For observer on the ground :

$R sin θ = m a$
$R cos θ = m g \Rightarrow a = g tan θ$
(a) Force to be applied on the wedge
$F = (M + m) a = (M + m) g tan θ$
(b) Force exerted by the wedge on the block
$= R = \frac{m g}{cos θ}$ or $R = m g sec θ$
II. For the observer on the wedge :
Pseudo force = ma towards left.
$∵$ the block appears to be at rest to him
$m a cos θ = m g sin θ$
$a = g tan θ$
$R = m g cos θ + m a sin θ$
$= m g cos θ + m g tan θ sin θ$
$= m g cos θ + m g . \frac{{sin}^{2} θ}{cos θ}$

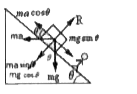
$= m g . \frac{({cos}^{2} θ + {sin}^{2} θ)}{cos θ}$
$R = \frac{m g}{cos θ} = m g sec θ$

Updated on:21/07/2023

A block of mass m is placed on a smooth wedge of incination $θ$ . The whole system s acelerated horizontally so tht the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
Amg
B $m \frac{g}{cos θ}$
C $m g cos θ$
D $m g tan θ$
A block of mass m is placed on a smooth wedge of inclination $θ$ . The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
A $m g cos θ$
B $m g sin θ$
C $m g$
D $\frac{m g}{cos θ}$
A block of mass m is placed on a smooth wedge of wedge angle $θ$ The whole system is accelerated horizontally so that the block does not slip on the wedge. The force (normal reaction) exerted by the wedge on the block has a magnitude:
A $m g tan θ$
B $\frac{m g}{cos θ}$
Cmg
D $m g cos θ$