In the above problem, the maximum length of the hanging part to prevent the chain from sliding down the incline is
m1gsin30=m2g+μm1gcos30
(L−x)g.12=xg+μ(L−x)g√3/2
(L−x)12=x+μ(L−x)√32
∴x=(1−√3μ)L(3−√3μ)
Similar Questions
A rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient of friction between chain and inclined plane is H, the maximum length of the hanging part to prevent the chain from falling vertically is 30°
View SolutionA rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient offriction between chain and inclined plane is μ, the maximum length of the lianging part to prevent the chain from falling vertically is:
View Solution
Knowledge Check
If a cylinder is rolling down the incline with sliding -
Aafter some time it may starts pure rollingBaftersometime it will start pure rollingCit may be possible that it will never start pure rollingDnone of theseThe force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is
A1√2B1√3C12D13The force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is .
A1√2B1√3C12D13
A uniform chain of length L is lying partly on a table, the remaining part hanging down from the edge of the table. If the coefficient of friction between the chain and the table is 0.5 what is the minimum length of the chain that should lie on the table, to prevent the chain from slipping down to the ground.
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
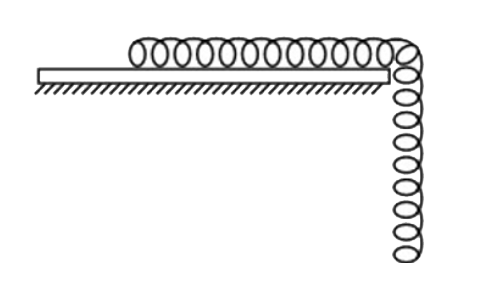
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?

View SolutionA uniform metal chain is placed on a rough table such that the one end of chain hangs down over the edge of the table, when one-third of its length hang over the edge, the chain starts sliding. Then the coefficient of static friction is
View SolutionA uniform metal chain is placed on a rough table such that the one end of chain hangs down over the edge of the table, when one-third of its length hang over the edge, the chain starts sliding. Then the coefficient of static friction is
View Solution
