All surfaces are smooth. The acceleration of mass m relative to wedge is
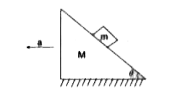
gsinθ
gsinθ+acosθ
gsinθ−acosθ
acosθ
The correct Answer is:B
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
108 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I
158 Videos
- KINETIC THEORY OF GASESBOOK - AAKASH SERIESCHAPTER - KINETIC THEORY OF GASESEXERCISE - Practice Exercise
15 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-3
43 Videos
Similar Questions
Knowledge Check
All surfaces are smooth. The acceleration of mass m relative to the wedge is
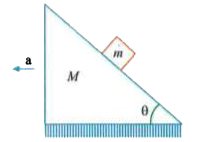AgsinθBgsinθ+acosθCgsinθ−acosθDacosθAll surfaces are smooth The acceleration of mass m relative to the wedge is
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
In given figure all surfaces are smooth. The ratio of forces exerted by the wedge on mass 'M' when force 'F' is not applied and when 'F' is applied such that 'M' is at rest with respect to wedge is:
View SolutionIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
View SolutionIn the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
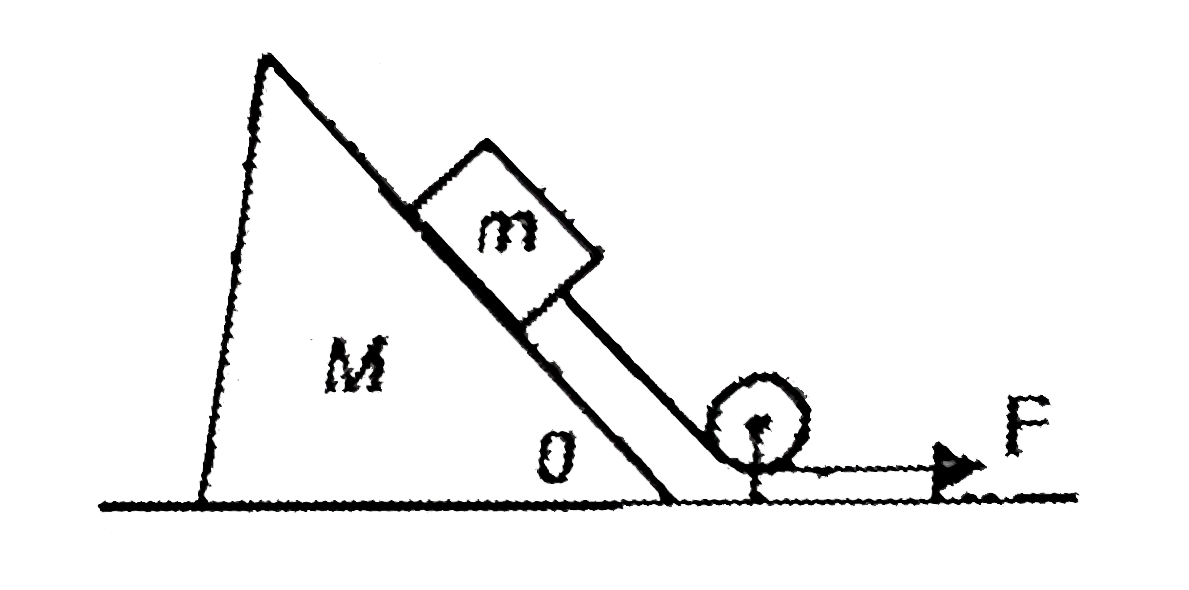
View SolutionIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
View SolutionA block of mass m placed on the inclined surface of wedge of mass M. Block is clamped between two smooth vertical support such that it can move along vertical If all contact surface are smooth then acceleration of wedge is:
View Solution