Coefficient of restitution during the collision is changed to 1/2 keepting all other parameters unchanged. What is the velocity of the ball B after the collision ?
The correct Answer is:B
Similar Questions
Consider a horizontal surface moving vertically upward with velocity 2ms−1. A small ball of mass 2 kg is moving with velocity (2ˆi−2ˆj)ms−1 If the coefficient of restitution and coefficient of friction are 12and13 respectively, find the horizontal velocity (in ms−1) of the ball after the collision.
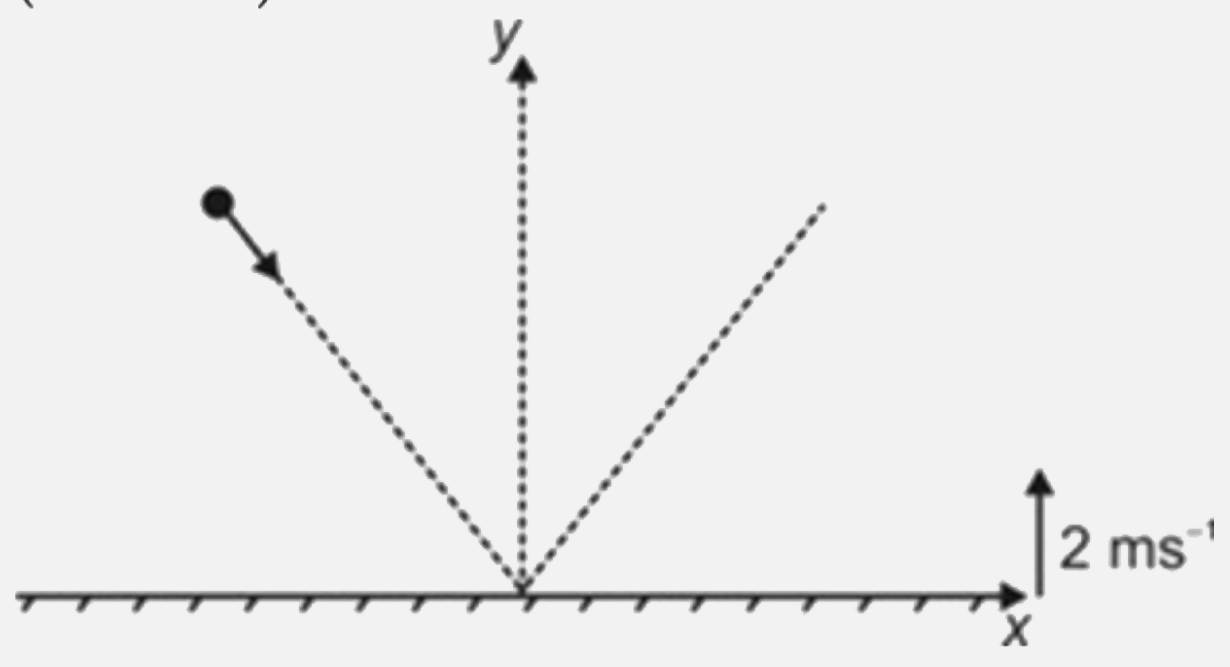
View SolutionConsider a horizontal surface moving vertically upward with velocity 2ms−1. A small ball of mass 2 kg is moving with velocity (2ˆi−2ˆj)ms−2 If the coefficient of restitution and coefficient of friction are 12and13 respectively, find the horizontal velocity (in ms−1) of the ball after the collision.

View Solution
Knowledge Check
A ball A of mass 3m is placed at a distance d from the wall on a smooth horizontal surface Another ball B of mass m moving with velocity u collides with ball A. The coefficient of restitution between the balls and the wall and between the balls is e
(a) the velocity of ball B after collision is u(3e−1)4.
(b) the velocity of ball B after collision is u(2e−1)4.
( c) after collision, ball A will have away by distance d(2e−1)(2e−1) during the time ball B returns back to wall.
(d) after collision, ball A will move away by distance d(e−1)(3e−1) during the time ball B returns back to wall.Aa,dBa,cCb,dDc,dA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.
 Athe angle θ=tan−1(1√2)BThe speed of the ball after the collision =4√2ms−1CThe total loss in kinetic energy during the collision is 8J.DThe ball hits the inclined plane again while travelling vertically downward.
Athe angle θ=tan−1(1√2)BThe speed of the ball after the collision =4√2ms−1CThe total loss in kinetic energy during the collision is 8J.DThe ball hits the inclined plane again while travelling vertically downward.A ball of mass m moving with a constant velocity strikes against a ball of same mass at rest. If e= coefficient of restitution, then what will the the ratio of the velocities of the two balls after collision?
A1−e1+eBe−1e+1C1+e1−eD2+ee−1
A ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionA ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.

View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
