A sphere of radius 'a' subtends an angle 60∘ at a point P. Then the distance of P from the centre of the sphere is.Solution in Telugu
a√3
2a
a√32
2a√3
The correct Answer is:D
Step by step video, text & image solution for A sphere of radius 'a' subtends an angle 60^(@) at a point P. Then the distance of P from the centre of the sphere is. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - HEIGHTS AND DISTANCESEXERCISE - PRACTICE SHEET (EXERCISE HEIGHTS AND DISTANCES) (LEVEL- I (MAIN) SINGLE ANSWER TYPE QUESTIONS)30videos
HEIGHTS AND DISTANCES
- BOOK - AAKASH SERIESCHAPTER - HEIGHTS AND DISTANCESEXERCISE - LECTURE SHEET Exercise-I (Straight Objective Type Questions)27videos
HEIGHTS AND DISTANCES
- BOOK - AAKASH SERIESCHAPTER - HEIGHTS AND DISTANCESEXERCISE - PRACTICE SHEET Exercise-I (Level-II) (Straight Objective Type Questions)13videos
HEIGHTS AND DISTANCES
- BOOK - AAKASH SERIESCHAPTER - FUNCTIONS EXERCISE - PRACTICE EXERCISE50videos
FUNCTIONS
- BOOK - AAKASH SERIESCHAPTER - HYPERBOLIC FUNCTIONS EXERCISE - PRACTICE SHEET EXERCISE-II (STRAIGHT OBJECTIVE TYPE QUESTIONS)18videos
HYPERBOLIC FUNCTIONS
Similar Questions
A man standing on a level plane observes the anlge of elevation of top of pole to be 'α'. He walks a distance equal to double the height of pole towards it and finds that the elevation in 2α then α =
02:46View SolutionA tower of height 30 metres casts a shadow of length 40 meters at a certain instant. When the sun's elevation increases by Tan−117, the length of the shadow cast by the tower, in meters is
08:56View SolutionThe angle of elevation of the top of a tower standing on a harzontal plane from the two points lying on a line passing through the foot of the tower at distances a and b respectively are complementary angles. If the line joining the two points sutends an angle θ at the top of the tower, then sinθ is
05:06View SolutionIf f(x)=3x−75x−3 then (fof)(x)=
04:42View SolutionThe domain of cosh−1(2x) is
04:20View SolutionA sphere of radius a subtends an angle 60^(@) at a point P. Then the distance of P from the centre of the sphere is.
06:41View SolutionA uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
02:06View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is p. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and centre of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View SolutionP is a point at a distance r from the centre of a solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ?
05:02View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
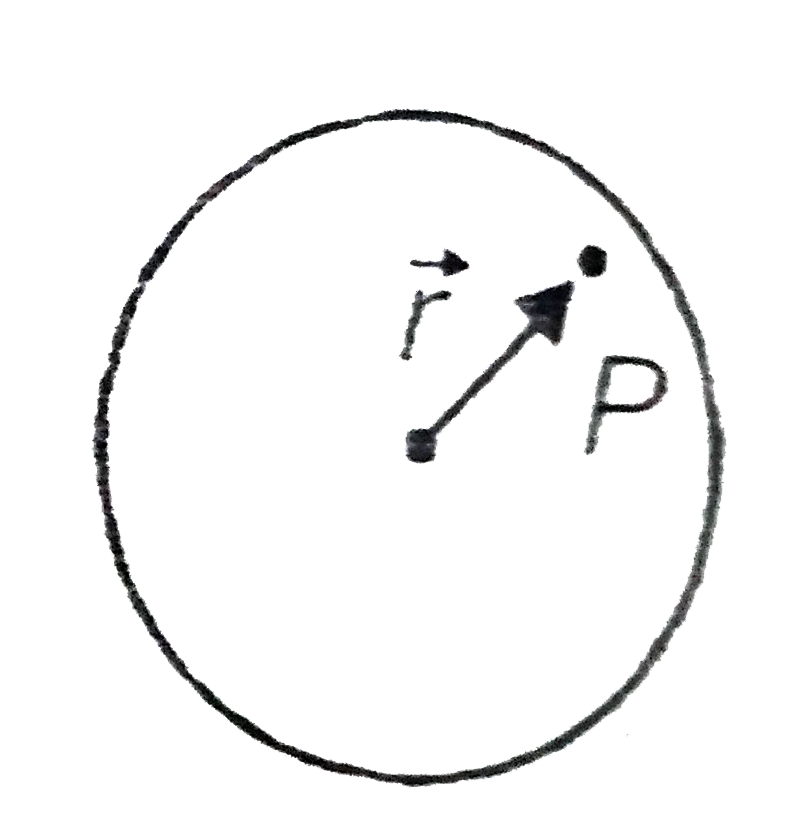
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.View SolutionIf charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
View SolutionIf charge q induced on outer surface of sphere of radius R, then intensity at point P at distance S from centre is
View SolutionThe centre of neutral conducting sphere of radius "R" is at distance 'd' from a point charge "Q" .The potential of the sphere is
01:51View SolutionP is a point at a distance r from the centre of a solid sphere of radius a. The gravitational potential at P is V. If V is plotted as a function of r, which is the correct curve ?
06:56View Solution

