A point sized sphere of mass 'm' is suspended from a point a string a string of length 'l'. It is then pulled to a side till the string is horizontal and released. As the mass passes through the portion where the string is vertical, magnitude of its angular momentum is
ml√gl
ml√2gl
ml√gl/2
ml√3gl
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - III) (LEVEL - II Straight Objective Type Questions)
3 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - III) (LEVEL - II More than One correct answer Type Questions)
5 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - II) (LEVEL - II Linked Comprehension Type Questions)
3 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A bob is suspended from an ideal string of length 'l'. Now it is pulled to a side through 60∘ to vertical and whirled along a horizontal circle. Then its period of revolution is
View SolutionA particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View Solution
Knowledge Check
A particle of mass m is suspended from a fixed O by a string of length L. At t=0, it is displaced from its equilibrium position and released. The graph which shows the variation of the tension T in the string with time t is :
 A
A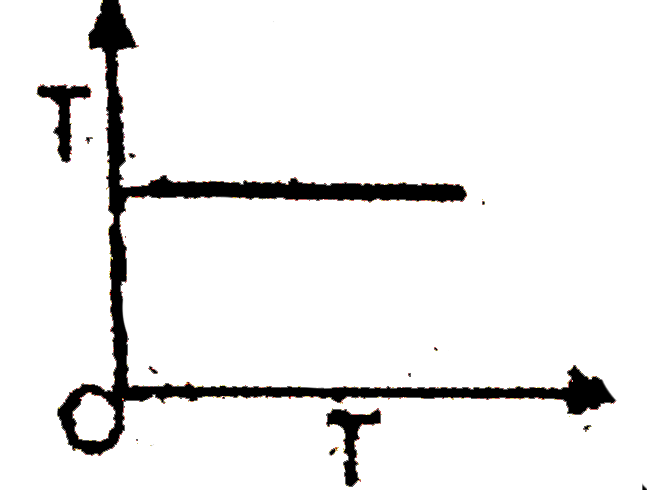 B
B C
C D
D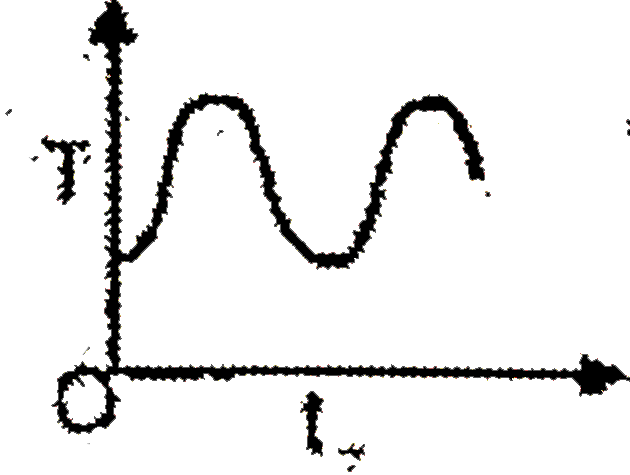
A uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :
 AmgBmg4Cmg2Dmg3
AmgBmg4Cmg2Dmg3A particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
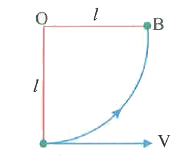 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2gl
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionConsider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View SolutionA pendulum consisting of a small sphere of mass m, suspended by a inextensible and massless string of length 1 , is made to swing in a vertical plane. If the breaking strength of the string is 2 mg, then the maximum angular amplitude of the displacement from the vertical can be
View SolutionA stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
View Solution
