Two horizontal discs of different radii are free to rotate about their central vertical axes. One is given some angular velocity, the other is stationary. Their rims are now brought in contact. There is friction between the rims
the force of friction between the rims will disappear when the discs rotate with equal angular speeds.
the force of friction between the rims will disappear when they have equal linear velocities
the angular momentum of the system will conserved
the rotational kinetic energy of the system will not be conserve
The correct Answer is:B, D
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - III) (LEVEL - II Integer Type Questions)8videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - I Straight Objective Type Questions)26videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - III) (LEVEL - II Straight Objective Type Questions)3videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)6videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers20videos
ROTATIONAL MECHANICS
Similar Questions
Two horizontal discs A and B of radii r and 2r having moments of inertia I and 4I about their axes. Initially, disc A is rotating with ω0 and disc B is at rest. Their rims are now brought in contact. The discs first slip over each other at the contact but slipping finally ceases due to the fricition between them. Find the angular speeds of the discs after the slipping ceases. Also, find the loss in kinetic energy.
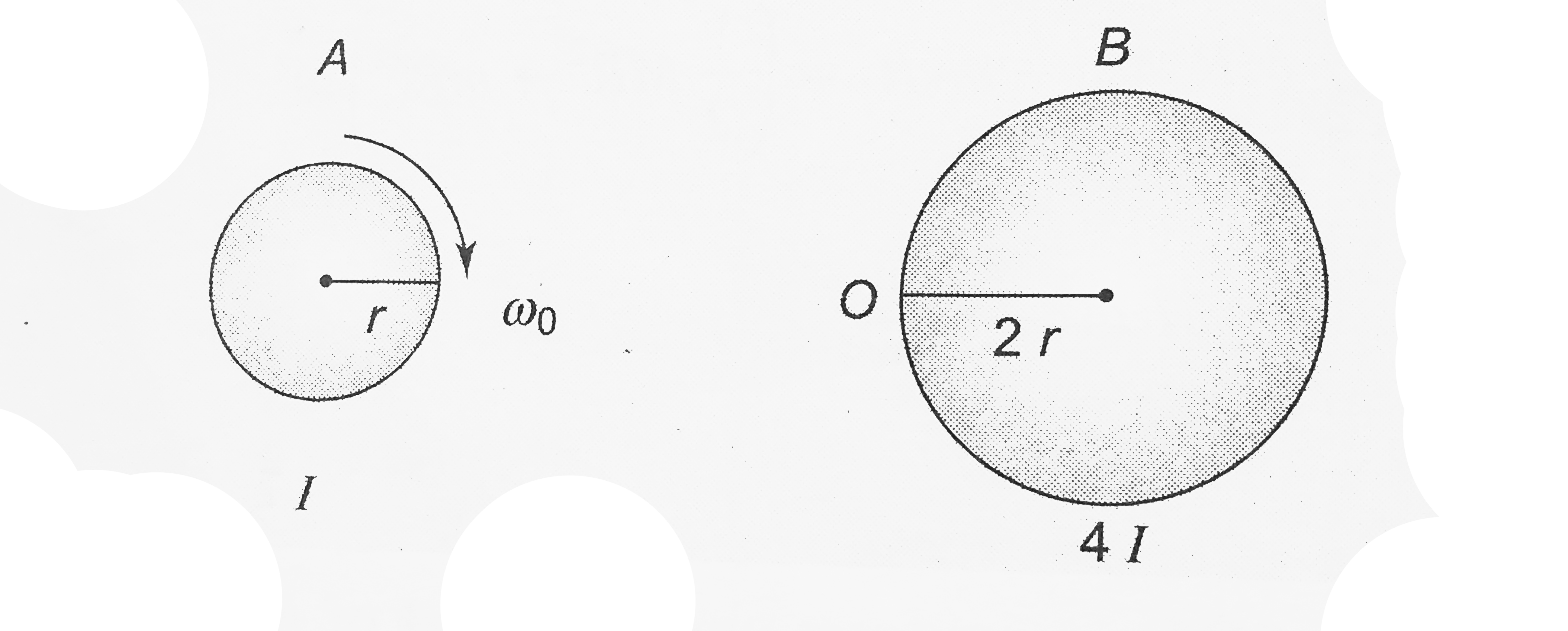 View Solution
View SolutionTwo discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
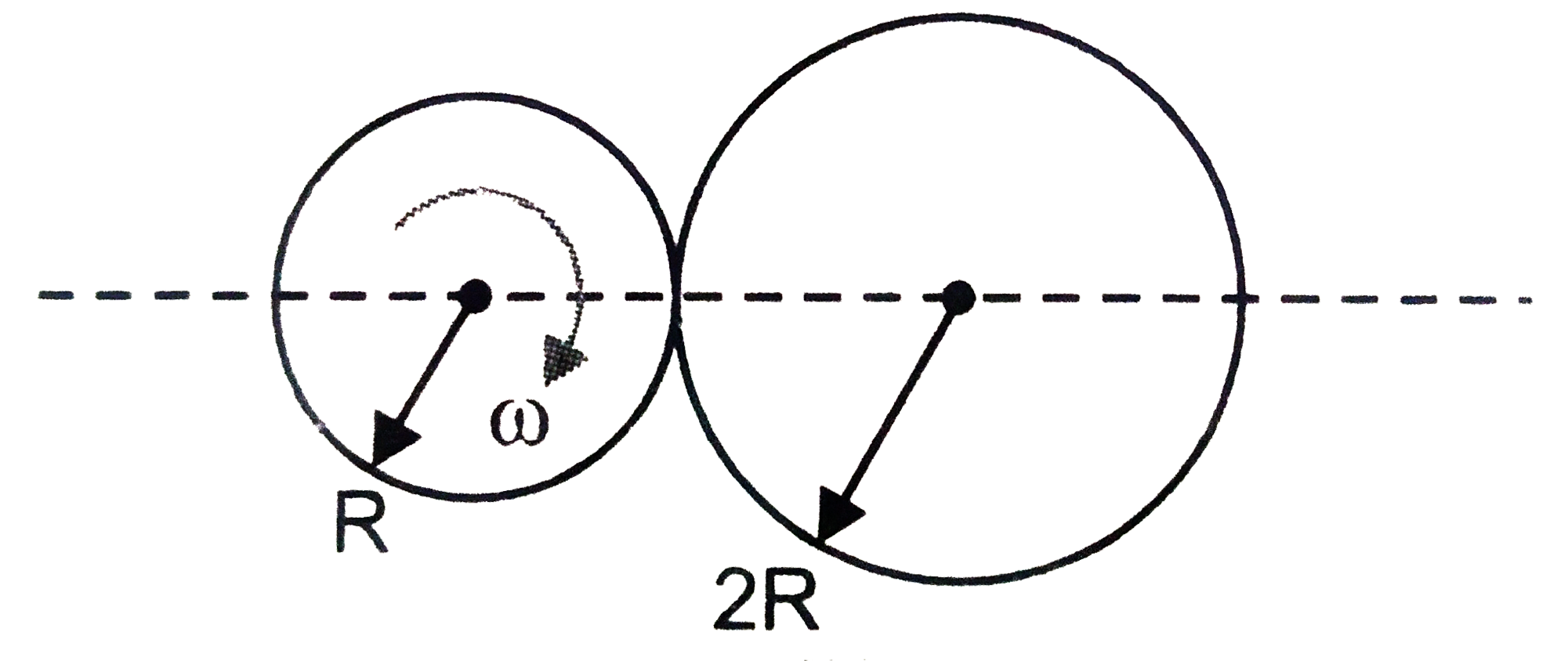 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
Ano friction exists between te disc and the ringBthe angular momentum of the system is conservedCthe final common angular velocity is 12ωDall of the above - Question 2 - Select One
Two discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
AI1ω1+I1ω2I1+I2BI2ω1+I1ω2I1+I2CI1ω1−I2ω2I1−I2DI2ω1−I1ω2I1−I2
Two discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
 View Solution
View SolutionA horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A ring having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.
 View Solution
View SolutionA uniform dis of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Find
(A) the angular velocity of the disc.
(B) the impulse on the particle due to disc
( C) the impulse on the disc due to hinge.View Solution

