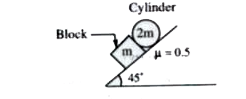
A block of mass m and a cylinder of mass 2m are released on a rough inclined plane, inclined at angle $θ = 45^{\circ}$ with the horizontal. The coefficient of friction for all the contact surface is $0.5$ Find the accelerations of the block and the cylinder. Assume pure rolling $3 g / x \sqrt{2}$ where 'x' is

Text Solution

Verified by Experts

The correct Answer is:5

Updated on:21/07/2023

A solid cylinder of mass $m$ rolls without slipping down an inclined plane making an angle $θ$ with the horizontal. The frictional force between the cylinder and the incline is
A $m g sin θ$
B $\frac{m g sin θ}{3}$
C $m g cos θ$
D $\frac{2 m g sin θ}{3}$
A solid cylinder of mass $m$ and radius $r$ is rolling on a rough inclined plane of inclination $θ$ . The coefficient of friction between the cylinder and incline is $μ$ . Then.
Africtional force is always $μ m g cos θ$
Bfriction is a dissipative force
Cby decreasing $θ$ , frictional force decreases
Dfrictiona opposes translation and supports rotation.
A block of mass m is placed on a rough plane inclined at an angle $θ$ with the horizontal. The coefficient of friction between the block and inclined plane is $μ$ . If $θ < {tan}^{- 1} (μ)$ , then net contact force exerted by the plane on the block is :
Amg cos $θ$
Bmg
Cmg sin $θ$
DNone of these