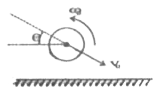
A spherica ball of radius R and mass m collides with a plank of mass M kept on a smooth horizontal surface Just before impact the centre of the ball has a velocity V0 and angular velocity ω0 as shown in the figure. After the impact, the normal velocity is reversed with same magnitude and the ball stops rotating after the impact. The coefficient of friction between the and the plank is μ. Assume that the plank is larger enough. The distance on the plank between first two impacts of the ball is 4V0Rω0βg(1+mM) Find the value of β

The correct Answer is:3
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Straight Objective Type Questions
37 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Matrix Matching Type Questions
3 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View Solution
Knowledge Check
A solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
 AdecraseBincreaseCremains constantDnone of these
AdecraseBincreaseCremains constantDnone of theseA ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is
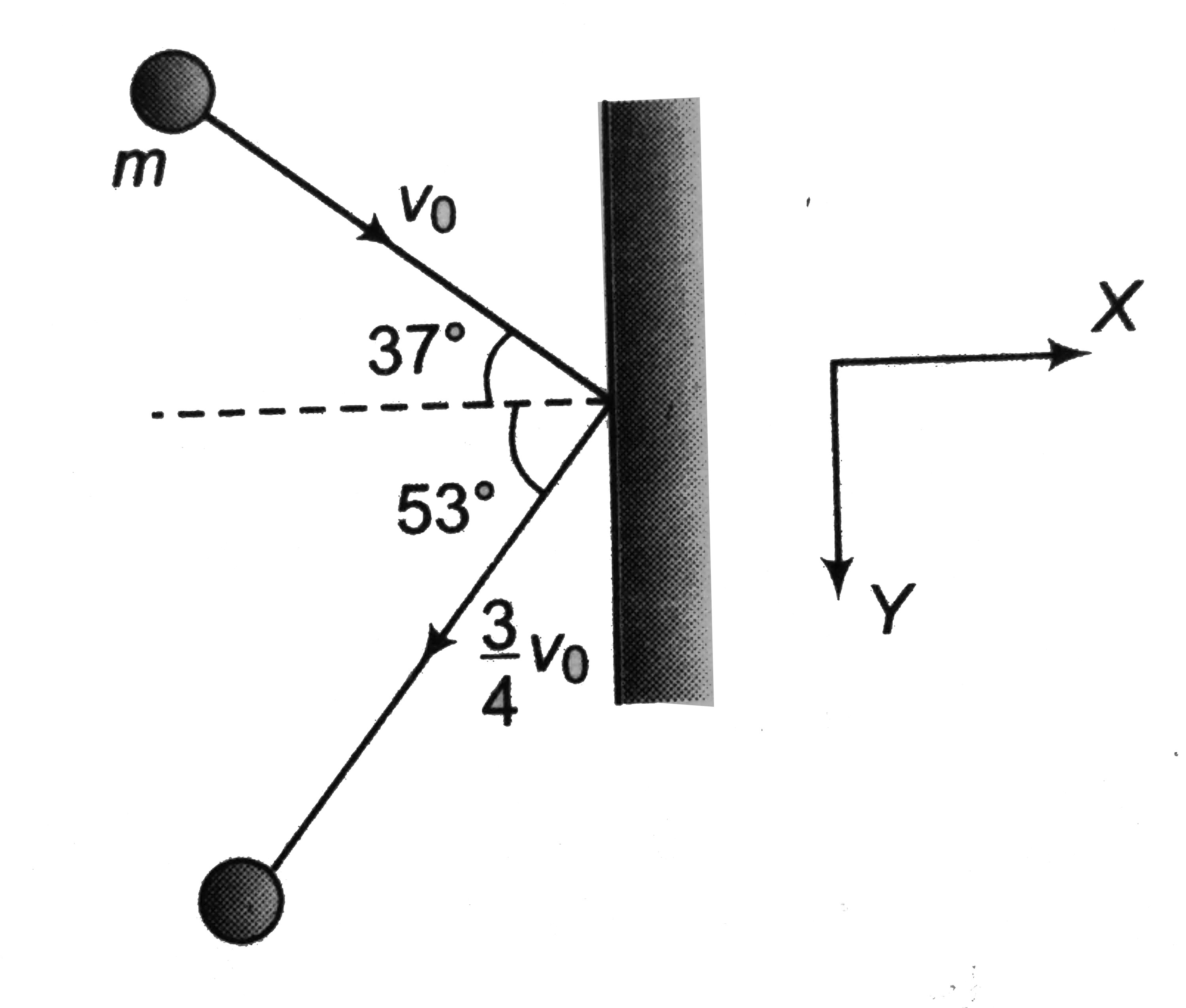 A−m2v0ˆjB−34mv0ˆiC−54mv0ˆiDNone of the above
A−m2v0ˆjB−34mv0ˆiC−54mv0ˆiDNone of the aboveA solid shperical ball of mass m and radius R is present on a rough horizontal surface. A person hit the ball at distance h above the centre of the ball as shown in the figure. Find out the h such that the ball starts pure rolling just after impact.
 Ah=R5Bh=3R5Ch=RDh=2R5
Ah=R5Bh=3R5Ch=RDh=2R5
A billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View SolutionA ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is

View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
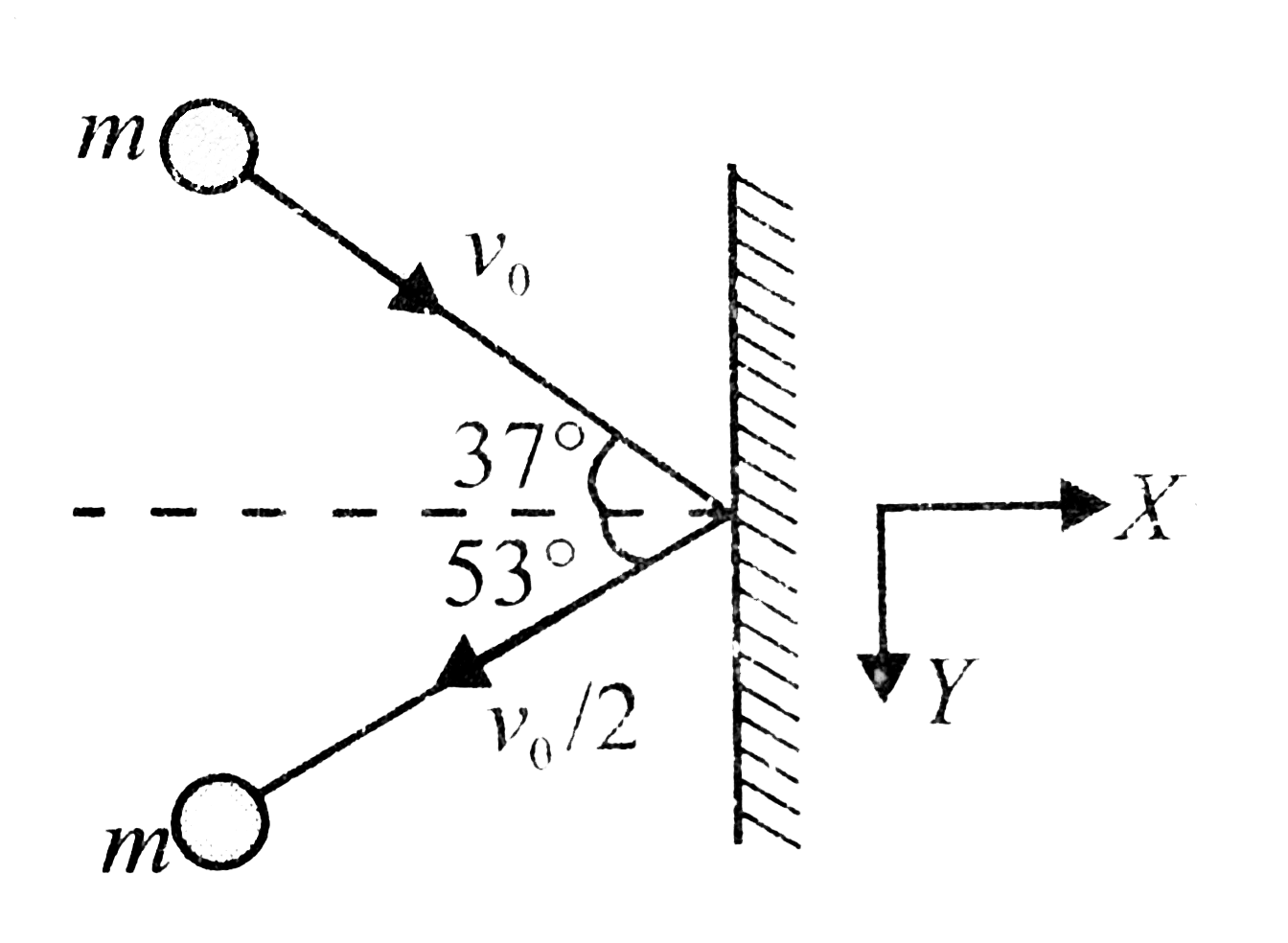
View SolutionA ball of mass m = 1 kg rolling without slipping, strikes a smooth vertical wall and comes back. Before the impact the velocity of the ball is v1=10 cm/s and just after the impact v1=8 cm/s. Find the loss in energy of ball during the impact.
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is

View Solution
