A uniform circulr disc has radius R and mass m. A particle also of mass m is fixed point A on the edge of the disc as shown in the fig. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then aloowed to fall so that it starts rotaing about PQ. Then linear speed of the particle as it reaches its lowest posirion √xgR where 'x' is
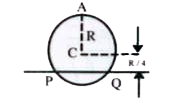
The correct Answer is:5
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Straight Objective Type Questions
37 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Matrix Matching Type Questions
3 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A uniform circula disc has radius R and mass m. A particle also of mass m, is fixed at a point A on the edge of the disc as shown in figure. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially, the disc is held vertical with the point A at its highes position.
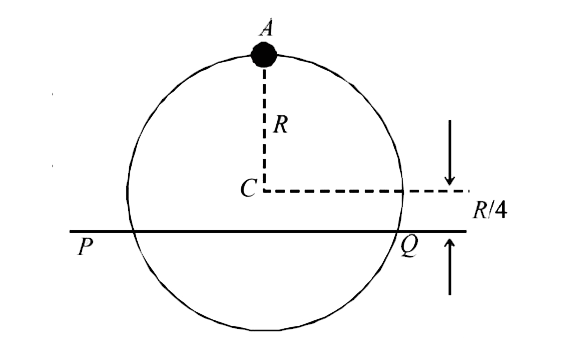
View SolutionA uniform circular disc has radius R and mass m. A particle also of mass m is fixed at a point A on the wedge of the disc as in fig. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then allowed to fall so that it tarts rotating about PQ. Find the linear speed of the particle at it reaches its lowest position.
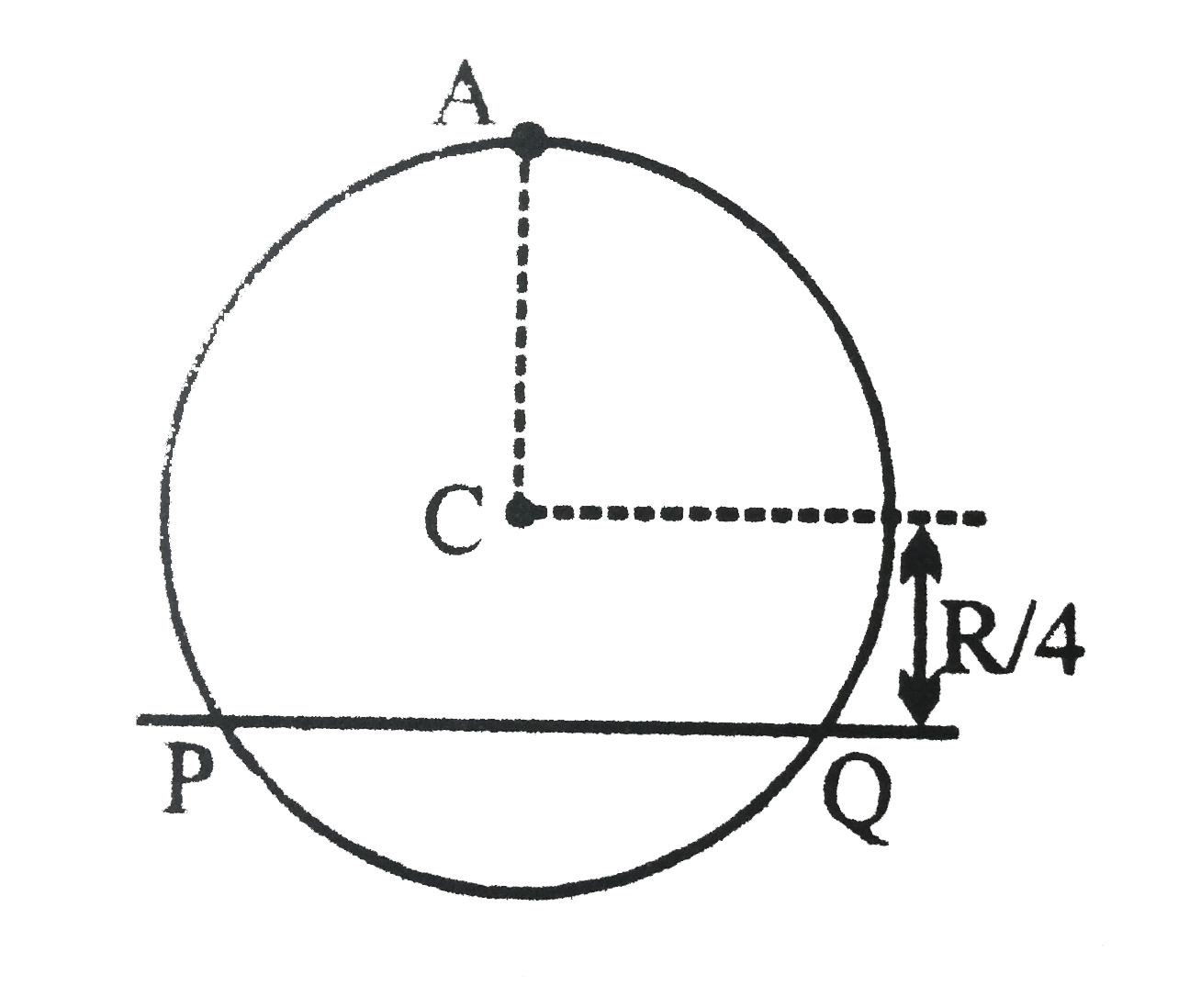 .
.
View Solution
Knowledge Check
A quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
 A12mR2ω2B14mR2ω2C18mR2ω2D116mR2ω2
A12mR2ω2B14mR2ω2C18mR2ω2D116mR2ω2A disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at this instant isAMg5(R2+2r2)×√9(R2+6r2)2+(4R2)2BMg5(R2+2r2)×3(R2+6r2)C4Mg5(R2+2r2)×R2DMg5(R2+2r2)×4R2
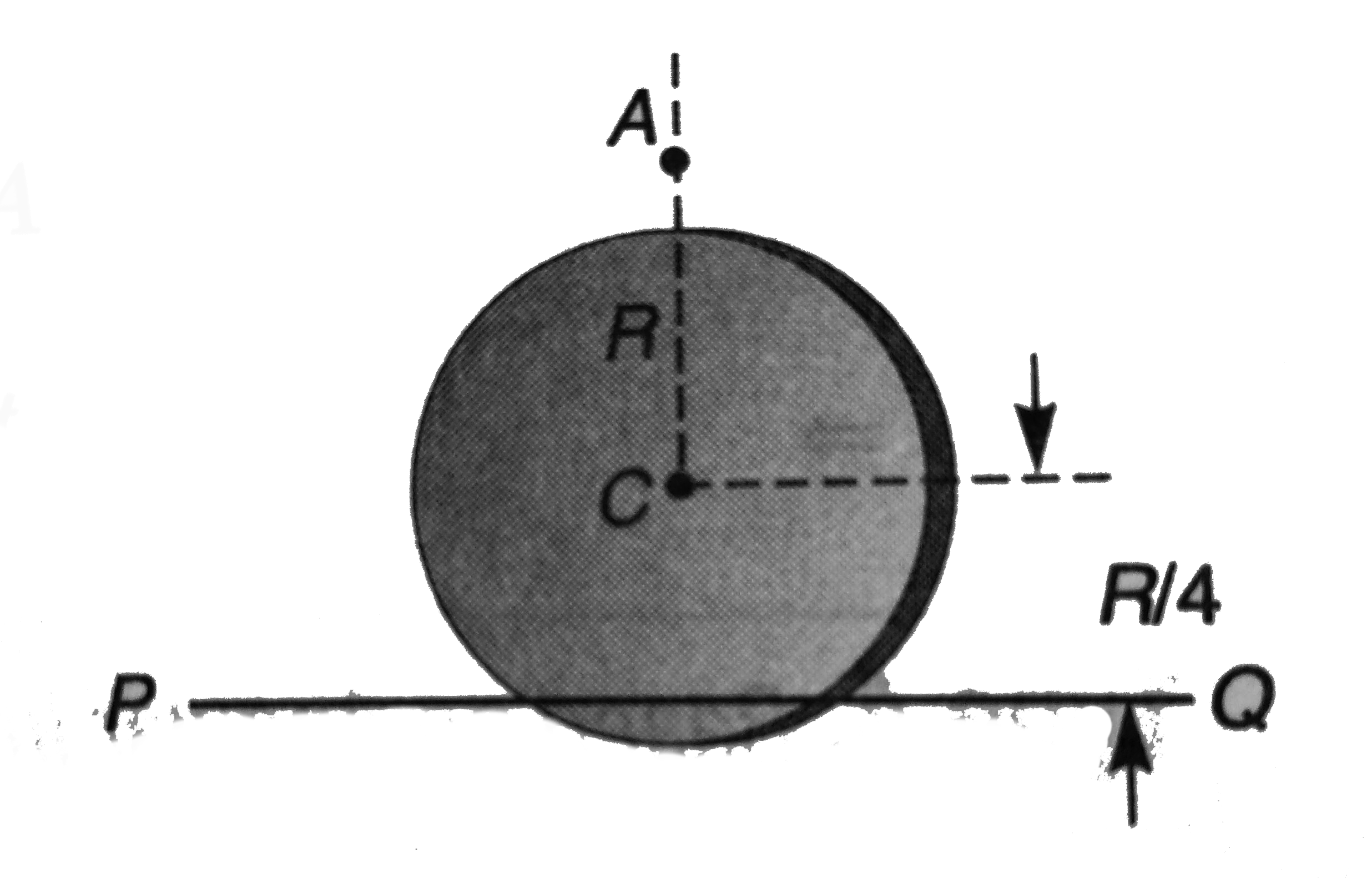
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View Solution
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View Solution
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is

View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View Solution
