A hollow sphere of radius R/4 is released from the top of a fixed sphere of radius R as shown. The angle θ made by the radius vector at the instant when smaller sphere leaves contact with the bigger sphere is (assume pure rolling of hollow sphere without slipping) cos−1(1010+x) where 'x' is
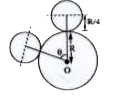
The correct Answer is:7
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Straight Objective Type Questions
37 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Matrix Matching Type Questions
3 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A uniform sphere of radius R16 starts rolling down without slipping from the top of another sphere of radius R=1m. The angular velocity of the sphere of in rads−1, after it leaves the surface of the larger sphere is 8xn. Where n=--
View SolutionA solid sphere hollow sphere disc, ring and hollow cylinder are relased from the top of a fixed inclined when all of them have same mass and radius

View Solution
Knowledge Check
A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
 Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.
Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.A hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Now the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would be
A3V2BV4CV2DV
A solid sphere hollow sphere disc, ring and hollow cylinder are relased from the top of a fixed inclined when all of them have same mass and radius

View SolutionA hollow sphere is released from the top of an inclined plane of inclination θ and length L. If a hollow sphere rolls without slipping, what will be its speed when it reaches the bottom?
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Now the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would be
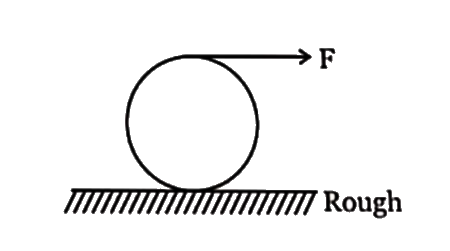
View SolutionA solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
View SolutionA uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View Solution
