From a solid hemisphere of radius 'R' a cone of a base radius 'R' and height 'R' is removed as shown in the figure. The moment of inertia of the remainng body about an axis BB' in the plane of the base and passing through the centre 'O' is $I_{0}, I_{1}$ is the moment of inertia about AA' which is parallel to BB' and $I_{2}$ is moment of inertia about an axis perpendicular to BB', and passing through 'O', then

A

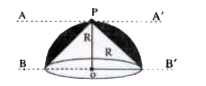
$I_{1} = I_{0}$

B

$I_{2} = 2 I_{0}$

C

$I_{1} = \frac{I_{0}}{2}$

D

$I_{2} = 3 I_{0}$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From a uniform circular disc of radius R and mass 9M, a small disc of radius $\frac{R}{3}$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :

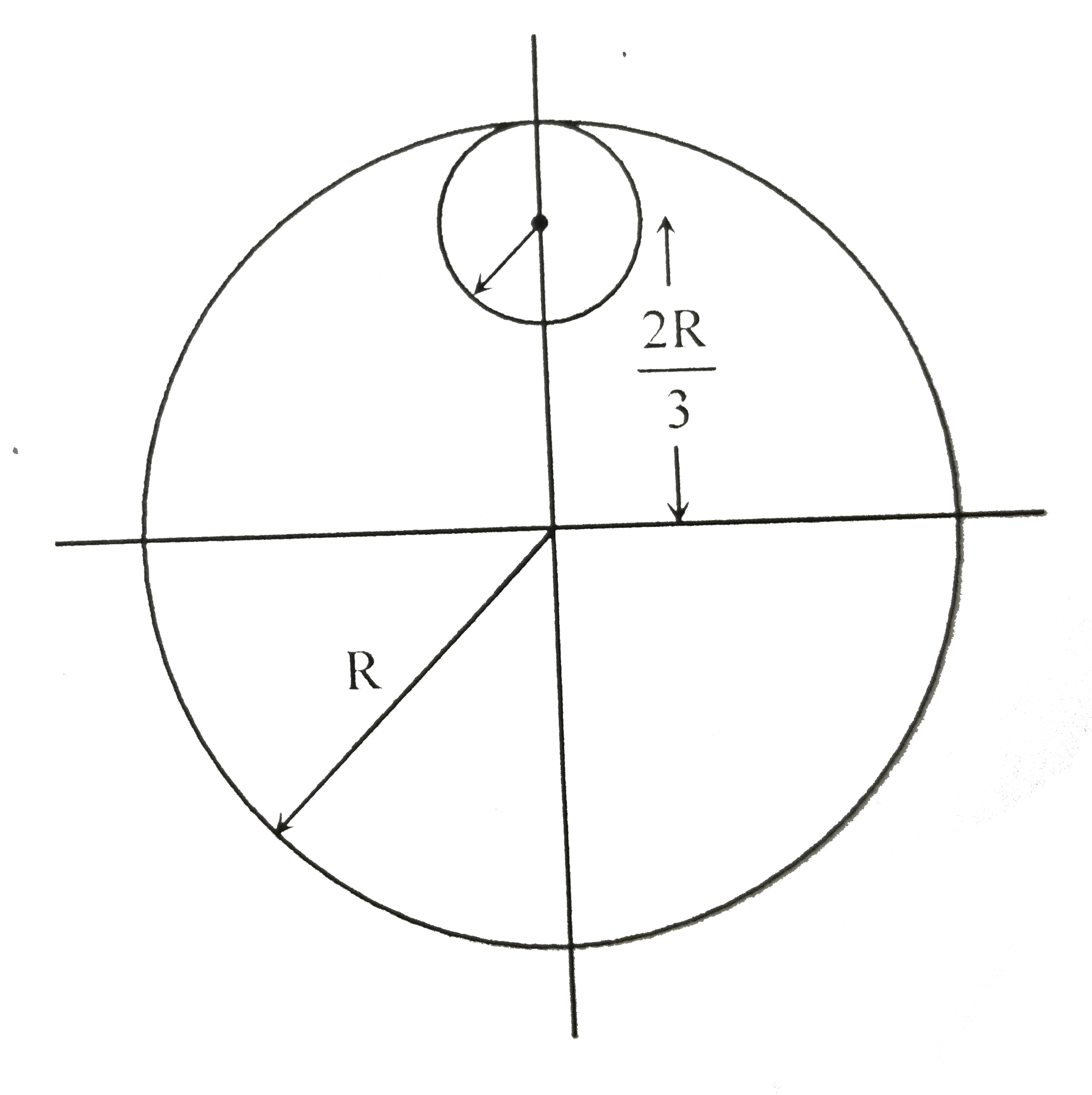A $4 M R^{2}$
B $\frac{40}{9} M R^{2}$
C $40 M R^{2}$
D $\frac{37}{9} M R^{2}$
Question 2 - Select One
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

A $4 M R^{2}$
B $\frac{40}{9} M R^{2}$
C $40 M R^{2}$
D $\frac{37}{9} M R^{2}$
Question 3 - Select One
Moment of inertia of disc about the tangent parallel to plane is I. The moment of inertia of disc about tangent and perpendicular to its plane is
A $M R_{n}^{2}$
B $\frac{M R_{n}^{2}}{2 t}$
C $\frac{M r ω}{t}$
D $M r ω t$

AAKASH SERIES-ROTATIONAL DYNAMICS -PRACTICE SHEET (ADVANCED) Straight Objective Type Questions

Home
Ask Doubt
Profile