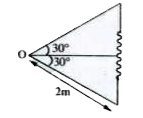
Two identical rods each of length 2 m and having same mass are connected from end to end by means of a spring of spring cpnstant (3+2√2) N/m. The other two ends of the rods are riveted to ground at O and are on a smooth horizontal surface. These two rods are free to rotate about the rivet on the horizontal surface. When the spring is in natural length the angle between the two rods is 60∘. From this position each rod is pulled away from each other by an angle of 15∘ and released. Then the force on the rivet when they come back to their initial position in Newton is
The correct Answer is:A
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Linked comprehension Type Questions
14 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Integer Type Questions
32 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View Solution
Knowledge Check
Two blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
A1B2C3D4A uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-
 A12π√2kMB12π√kMC12π√6kMD12π√24kM
A12π√2kMB12π√kMC12π√6kMD12π√24kMThe arrangement shown of a uniform rod of length l and mass m, pivoted at the centre and its two ends attached to two springs of spring constant K1 and K2 . The other end of springs are fixed to two rigid supports the rod which is free to rotate in the horizontal plane , is pushed by a small angle in one direction and released . Teh frequency of oscillation of the rod is
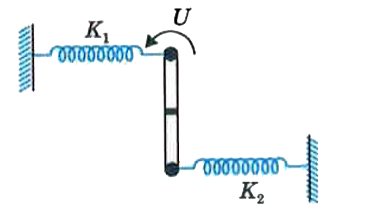 A12π√K1+K2mB12π√K1+K23mC12√3π√K1+K2mD√32π√K1+K2m
A12π√K1+K2mB12π√K1+K23mC12√3π√K1+K2mD√32π√K1+K2m
Two blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :

View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :

View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
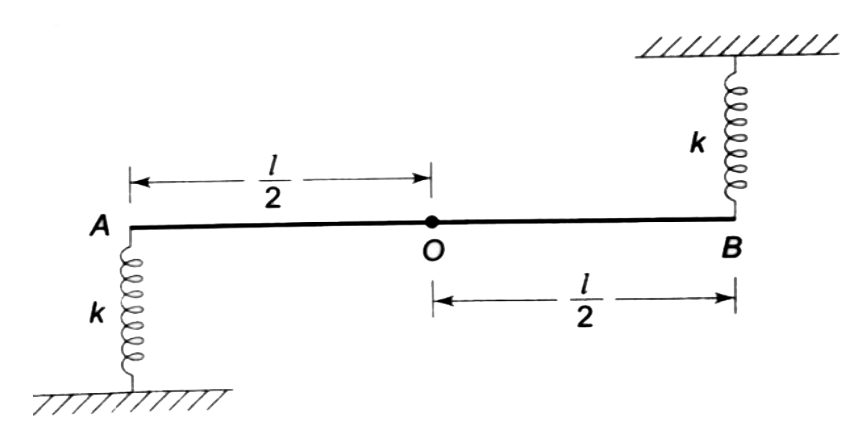
View SolutionA rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
View Solution
