Consider the pervious situation with VR>VbR Let VR=V1:VbR=V2
For this given situation the person
Can never reach the exactly opposite point A by swim.
May reach the elexactly point, if θ≠0
May (or) may not reach A depending on V1 & V2
Data insufficient to conclude whether person can reach opposite point A directly (or) not
The correct Answer is:A
Topper's Solved these Questions
- KINEMATICSBOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - LECTURE SHEET (EXERCISE-VII) (Relative motion) (Matrix-Matching Type Questions)
2 Videos
- KINEMATICSBOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - LECTURE SHEET (EXERCISE-VII) (Relative motion) (Integer Type Questions)
4 Videos
- KINEMATICSBOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - LECTURE SHEET (EXERCISE-VII) (Relative motion) (More than One correct answer Type Questions)
3 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) Integer Type Questions)
3 Videos
- KINETIC THEORY OF GASESBOOK - AAKASH SERIESCHAPTER - KINETIC THEORY OF GASESEXERCISE - Practice Exercise
15 Videos
Similar Questions
If the above question, the potential has correct relations as given=
A. VA>VB>VC>VD
B. VA>VB≥VC>VD
C. VD=VC=VB=VA
D. VC<VB>VA>VD
View SolutionThe electric potential at a point P due to two charges in fig (a) is V1 and in fig (b) is V2. Consider the given object to be a ring. What is the relation between V1andV2? Explain your answer.
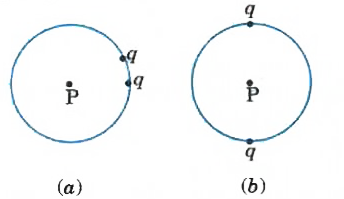
View Solution
Knowledge Check
In the following diagram if V2>V1 then
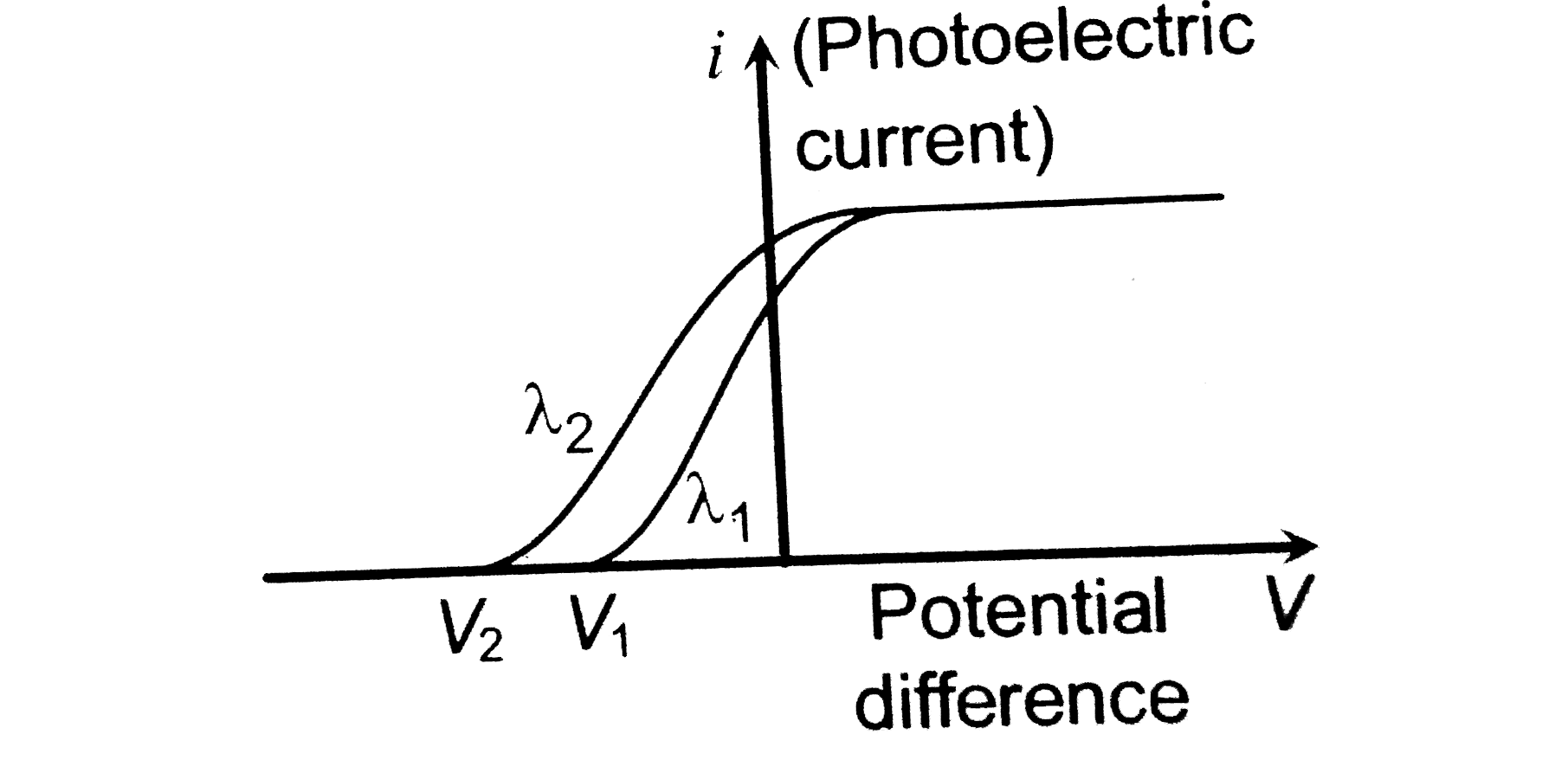 Aλ1=√λ2Bλ1<λ2Cλ1=λ2Dλ1>λ2
Aλ1=√λ2Bλ1<λ2Cλ1=λ2Dλ1>λ2A resistor R is connected in series with a coil. The system is subjected to an AC supply of peak voltage V0. If the peak voltages dropped across the resistor R and the coil are V1 and V2 respectively
(a) The powerr dissipated in the coil is
V20−V21−V222R
The power dissipated in the circuit is
V20+V21−V222R
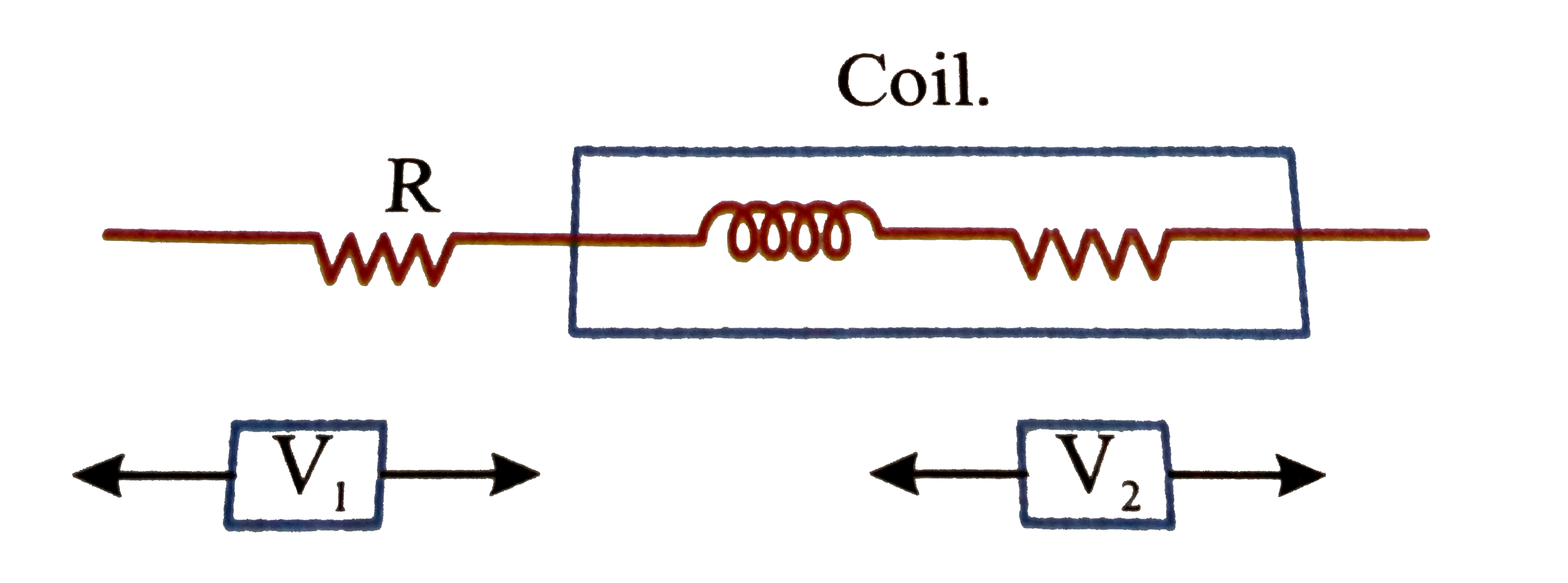 AOnly (a) is correctBOnly (b) is correctC(a),(b) are wrongD(a),(b) are correct
AOnly (a) is correctBOnly (b) is correctC(a),(b) are wrongD(a),(b) are correctConsider the following statements PVm=RT(1+BVm+BV2m+...) Then Vm .
Ais independent of temperatureBis equal to RTP to Boyle temperatureChas the dimension of molar volumeDNone of these
In a series LCR circuit V1=3V2 and Vc=2VR .If source has V=110 sin ot,find the peak voltage across the capacitance.
View SolutionThe electric field outside a charged long straight wire is given by E=1000rVm−1, and is directed outwards. What is the sign of the charge on the wire ? If two points A and B are situated such that rA=0.2m and rB=0.4m, find the value of (VB−VA).
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
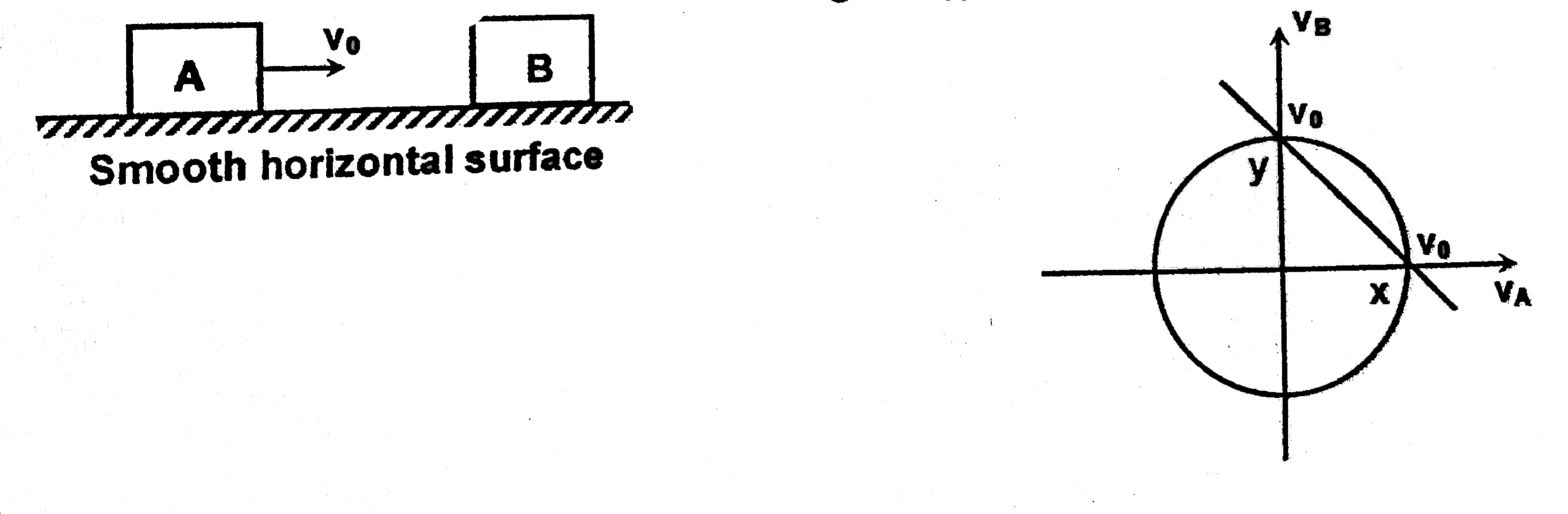
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is

View SolutionIn a series LCR circuit, VL=VC≠VR. What is the value of power factor ?
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
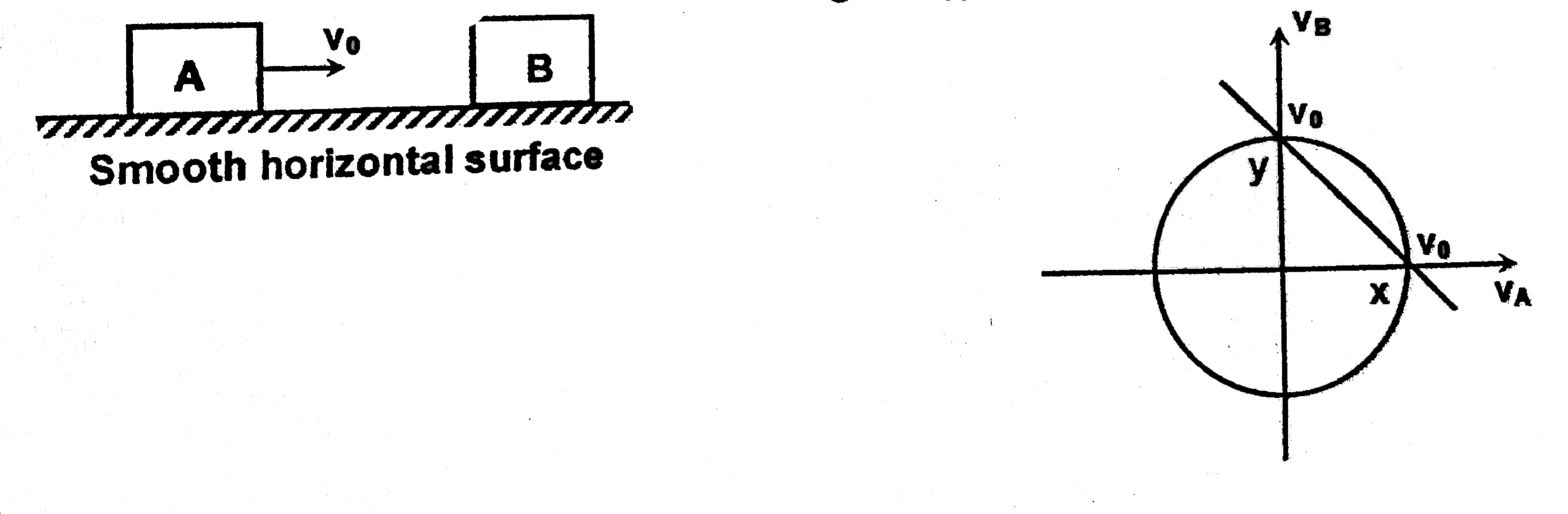
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is

View Solution
