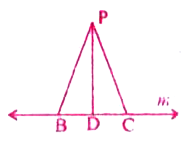
Of all the line segments drawn from a point P to a line l not containing P, let PD be the shortest. If B and C are points on l such that D is the mid-point of BC, prove that PB = PC.
Step by step video & image solution for Of all the line segments drawn from a point P to a line l not containing P, let PD be the shortest. If B and C are points on l such that D is the mid-point of BC, prove that PB = PC. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Of all the line segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC.
View SolutionIn Figure, lIIm and M is the mid-point of the line segment AB. Prove that M is also the mid-point of any line segment CD having its end-points on l and m respectively.
View SolutionOf all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
View SolutionIn Figure, l∣∣m and M is the mid-point of the line segment AB . Prove that M is also the mid-pooint of any line segment CD having its end-points on l and m respectively.
View SolutionOf all the lines segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC .
View SolutionAB ਇਕ ਰੇਖਾ ਖੰਡ ਹੈ ਅਤੇ ਰੇਖਾ l ਇਸ ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਹੈ। ਜੇਕਰ ਬਿੰਦੂ P,l ਉੱਤੇ ਹੋਵੇ ਤਾਂ ਸਿਧ ਕਰੋ ਕਿ P ਬਿੰਦੂ A ਅਤੇ B ਤੋਂ ਬਰਾਬਰ ਦੂਰੀ ਉੱਤੇ ਹੈ।
View SolutionP बिन्दु, जो m पर स्थित नहीं है से जितनी रेखाखंड खींची गई है उनमें PD सबसे छोटी है। यदि m पर B तथा C इस प्रकार बिन्दुएँ है कि BC का मध्य बिन्दु D है। साबित करें कि PB=PC.
View Solution
