Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 30∘ and at a distance 10 km further off from the mountain, along the same line, the angle of elevation is 15∘. (Use tan 15∘=0.27).Solution in Punjabi
Step by step video & image solution for Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 30^@ and at a distance 10 km further off from the mountain, along the same line, the angle of elevation is 15^@. (Use tan 15^@ = 0.27). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Some Applications Of TrignometryBOOK - MBDCHAPTER - Some Applications Of TrignometryEXERCISE - 271
20 Videos
- Some Applications Of TrignometryBOOK - MBDCHAPTER - Some Applications Of TrignometryEXERCISE - 267
2 Videos
- REAL NUMBERSBOOK - MBDCHAPTER - REAL NUMBERSEXERCISE - EXERCISE
83 Videos
- STATISTICSBOOK - MBDCHAPTER - STATISTICSEXERCISE - Exercise
54 Videos
Similar Questions
An aeroplane, when 3000 m high, passes vertically above another aeroplane at an instant when the angles of elevation of the two aeroplanes from the same point on the ground are 60∘ and 45∘ respectively. Find the vertical distance between the two aeroplanes.
View SolutionA straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30∘, which is approaching the foot of the tower with a uniform speed. Six secondslater, the angle of depression of the car is found to be 60∘. Find the further time taken by the car to reach the foot of the tower.
View SolutionUse Euclid's division algorithm to find HCF of : 36,84
View SolutionIn a city, the following weekly observations were made in a study of cost of living index for the year 1980-81.
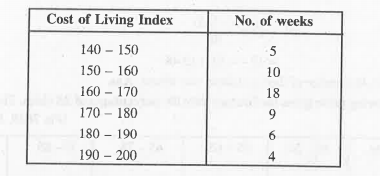 Calculate the mean weekly cost of living index by a suitable method.
Calculate the mean weekly cost of living index by a suitable method.
View SolutionOn a plane at some distance from its base a mountain is found to have an elevation of 60^(@) . At a station lying 900sqrt(3) further away from the mountain the angle is reduced to 30^(@). Find the height of the mountain.
View SolutionDetermine the height of a mountain if the elevation of its top at an unknown distance from base is 25^(@)10' and at a distance of 5km further off from the mountains,along the same line the angle of elevation is 15^(@)20' Give the answer in km correct to 2 decimals.
View SolutionDetermine the height of a mountain if the elevation of its top at an unknown distance from the base is 30o and at a distance 10km further off from the mountain, along the same line, the angle of elevation is 15o . (Use tan15o=0.27 )
View Solutionएक पहाड़ की चोटी से टॉवर के पाद का उन्नयन कोण 60∘ है तथा टॉवर के शीर्ष से पहाड़ की पाद पर उन्नयन कोण 30∘ है|यदि टॉवर की ऊंचाई 50 मीटर है तो पहाड़ की ऊंचाई ज्ञात कीजिए|
View Solution15 मीटर ऊँचे भवन के शीर्ष से मीनार के शीर्ष का उन्नयन कोण 30∘ है तथा भवन के पाद से मीनार के शीर्ष का उन्नयन कोण 60∘ है| तब मीनार की ऊंचाई तथा भवन से मीनार दी दुरी ज्ञात कीजिए|
View Solutionकिसी पर्वत के चरण से शिखर का उन्नयन कोण 45∘ है । पर्वत की और 30∘ के ढाल पर 1 km चलने के बाद उन्नयन कोण 60∘ हो जाता है । पर्वत की ऊँचाई ज्ञात करे ।
View Solutionयदि किसी पर्वत के आधार से एक निश्चित दूरी पर स्थित एक बिन्दु से इसके शिखर का उन्नयन कोण 30∘है तथा उसी सरल रेखा पर स्थित पहले बिन्दु से 10 किमी. की दूरी पर एक अन्य बिन्दु से शिखर का उन्नयन कोण 15∘है, तो पर्वत की ऊँचाई ज्ञात कीजिए |
(tan15∘=0.27)
View Solution15 मीटर ऊँचे एक भवन के शीर्ष से एक मीनार के शिखर का उन्नयन कोण 30∘ है | उसी भवन के आधार से मीनार के शिखर का उन्नयन कोण 60∘ है | मीनार की ऊँचाई तथा मीनार तथा भवन के बीच की दूरी ज्ञात कीजिए |
View Solutionएक मीनार के शीर्ष का उन्नयन कोण उसके पाद से 15 मी की दूरी पर 30∘है , तो मीनार की ऊँचाई है
View Solutionचट्टान की ऊँचाई ज्ञात कीजिए यदि इसके आधार से किसी अज्ञात दूरी से उसकी चोटी का उन्नयन कोण 45∘ है और चट्टान से 10 km अधिक दूरी से उसी रेखा में उन्नयन कोण 30∘ है ।
( (tan )30∘=0.5774 का प्रयोग कीजिए । )
View SolutionAt the foot of a mountain, the elevation of its summit is 45∘. After ascending 2 km towards the mountain upon an incline of 30∘, the elevation changes to 60∘. The height of the mountain is
View Solution
