A smooth pulley A of mass M0 is lying on a smooth table . A light string passes round the pulley and has masses M1andM2 attached to its ends , the two portions of the string being perpendicular to the edge of the table so that the masses hang vertically . Calculate the acceleration of the pulley .
Let the length of portions of string on the table be l0,l1andl2 as shown in figure .
Let mass M0 move to the right by x on the table ,M1goes down by y1andM2 goes up by y2
Then l0 becomes (l0−x) l_(1)becomes(l_(1)+y_(1))andl_(2) becomes(l_(2)-y_(2)).<br>Asthe≤n>hofstr∈grema∈sunchan≥d<br>2l_(0)+l_(1)+l_(2)=2(l_(0)-x)+l_(1)+y_(1)+l_(2)-y_(2)<br>or2x=y_(1)-y_(2)<br>D⇔.twicew.r.→t,<br>we≥t2(d^(2)x)/(dt^(2))=(d^(2)y_(1))/(dt^(2)-(d^(2)y_(2))/(dt^(2))<br>Ifa0,a1anda2 are acceleration of

M0,M1 and M2 respectively , then
2a0=a1−a2 ....(1)
For motion of M0,2T=M0a0 ....(2)
For motion of mass M1
M1g−T=M1a1 ....(3)
For motion of mass M2,
T−M2g=M2a2 ....(4)
Substituting values of a0,a1 and a2 from (2) ,(3) and (4) in equation (1) , we get
2(2TM0)=(g−TM1−(TM2−g),
4TM0=2g−T(1M1+1M2)i.e., (4/M_(0)+1/M_(1)+1/M_(2))T=2g<br>ThisgivesT=(2M_(0)M_(1)M_(2)g)/(4M_(1)M_(2)+M_(0)(M_(1)+M_(2))....(5)<br>:. Acee≤rationofp≤––––yAom(2)<br>a_(0) =(2T)/M_(0)=(4M_(1)M_(2)g)/(4M_(1)M_(2)+M_(0)(M_(1)+M_(2)) ....(6)
Similar Questions
A smooth pulley A of mass M0 is lying on a frictionless table. A massless rope passes round the pulley and has masses M1 and M2 tied to its ends, the two portions of the string being perpendicular to the edge of the table so that the masses hang vertically. Find the acceleration of the pulley.
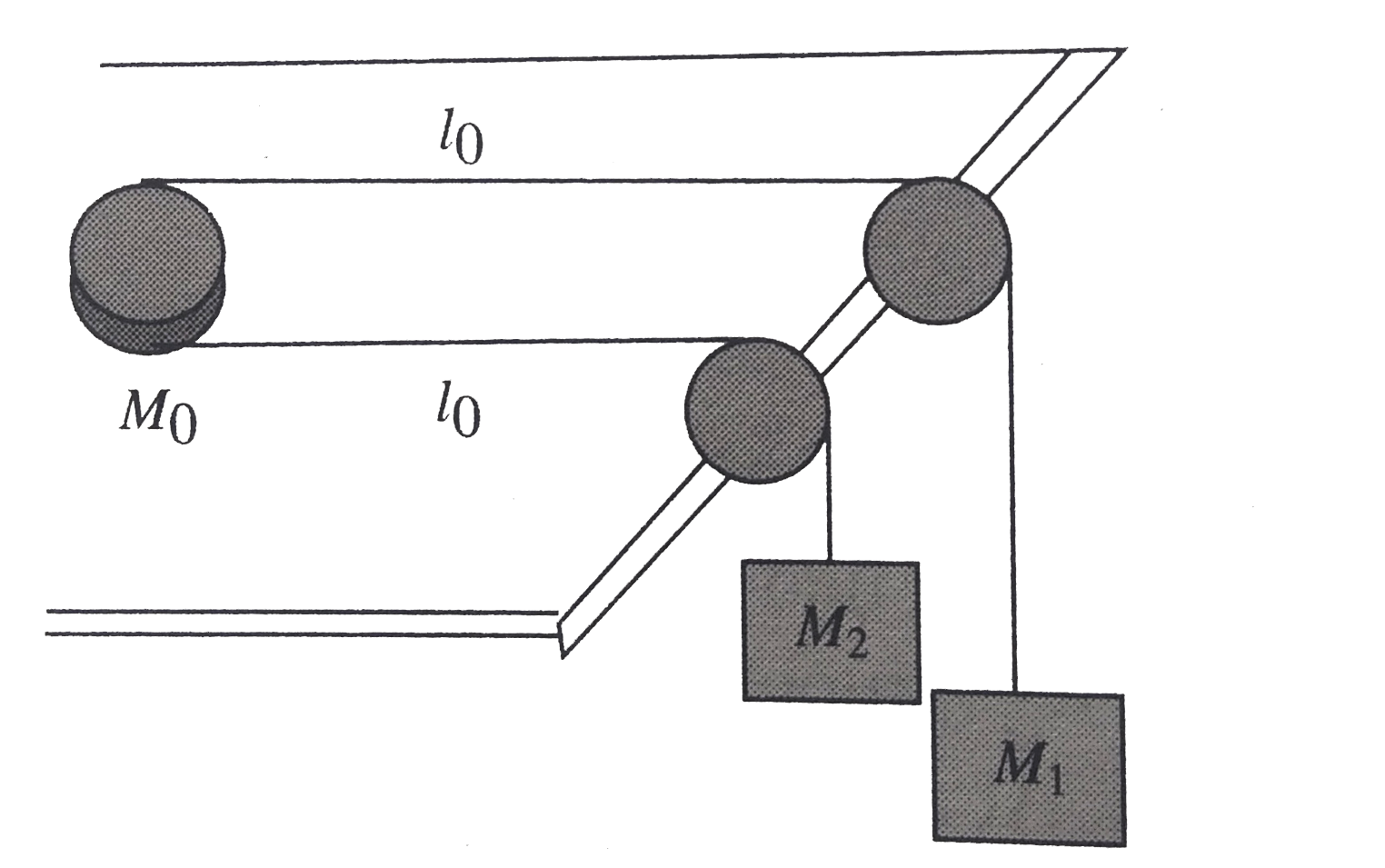
View SolutionA smooth pulley A of mass M0 is lying on a frictionless table. A massless rope passes round the pulley and has masses M1 and M2 tied to its ends, the two portions of the string being perpendicular to the edge of the table so that the masses hang vertically. Find the acceleration of the pulley.

View Solution
Knowledge Check
The masses (M+m) and (M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MTwo masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
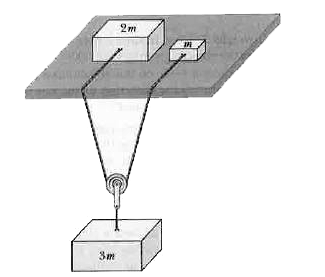
Two particles of masses m and 2m are placed on a smooth horizonttal table. A string, which joins these two masses, hangs over the edge supporting a pulley, which suspends a particle of mass 3m, as shown in Fig. 5-40. The pulley has negligible mass. The two parts of the string on the table are parallel and perpendicular to the edge of the table. The hanging parts of the string are vertical. Find the acceleration of the particle of mass 3m.
View SolutionWhat is the mechanical advantage of single fixed pulley:-

View SolutionTwo masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionA smooth massless string passes over a smooth fixed pulley. Two masses m1 and m2(m1>m2) are tied at the two ends of the string. The masses are allowed to move under gravity starting from rest. The total external force acting on the two masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of masses is
View Solution
