A particle is executing SHM along a straight line. Then choose the correct statement
Acceleration always decreases the speed of particle
Acceleration is maximum at mean position
Acceleration is minimum at extreme position
Acceleration varies with time and becomes maximum when particle is at rest
To solve the question about the particle executing Simple Harmonic Motion (SHM) along a straight line, we need to analyze the properties of SHM and the behavior of acceleration at different positions of the particle.
1. Understanding SHM:
- In SHM, a particle moves back and forth along a straight line about a mean position. The motion is periodic and can be described by sinusoidal functions.
2. Identifying Key Positions:
- The particle has two extreme positions (maximum displacement) and one mean position (equilibrium position).
- At the mean position, the particle's velocity is maximum, and its acceleration is zero.
- At the extreme positions, the particle's velocity is zero, and its acceleration is at its maximum.
3. Analyzing Acceleration:
- The acceleration a in SHM is given by the formula:
a=−ω2x
where ω is the angular frequency and x is the displacement from the mean position.
- This equation indicates that acceleration is directly proportional to the displacement and is always directed towards the mean position.
4. Evaluating the Options:
- Option 1: "Acceleration always decreases the speed of the particle."
- This is incorrect. Acceleration can increase the speed when the particle is returning from the extreme position.
- Option 2: "Acceleration is maximum at the mean position."
- This is incorrect. Acceleration is zero at the mean position.
- Option 3: "Acceleration is minimum at extreme position."
- This is incorrect. Acceleration is maximum at the extreme positions.
- Option 4: "Acceleration varies with time and becomes maximum when the particle is at rest."
- This is correct. The acceleration is maximum at the extreme positions when the particle is momentarily at rest.
5. Conclusion:
- The correct statement regarding the particle executing SHM is Option 4: "Acceleration varies with time and becomes maximum when the particle is at rest."
- In SHM, a particle moves back and forth along a straight line about a mean position. The motion is periodic and can be described by sinusoidal functions.
- The particle has two extreme positions (maximum displacement) and one mean position (equilibrium position).
- At the mean position, the particle's velocity is maximum, and its acceleration is zero.
- At the extreme positions, the particle's velocity is zero, and its acceleration is at its maximum.
- The acceleration a in SHM is given by the formula:
a=−ω2x
where ω is the angular frequency and x is the displacement from the mean position.
- This equation indicates that acceleration is directly proportional to the displacement and is always directed towards the mean position.
- Option 1: "Acceleration always decreases the speed of the particle."
- This is incorrect. Acceleration can increase the speed when the particle is returning from the extreme position.
- Option 2: "Acceleration is maximum at the mean position."
- This is incorrect. Acceleration is zero at the mean position.
- Option 3: "Acceleration is minimum at extreme position."
- This is incorrect. Acceleration is maximum at the extreme positions.
- Option 4: "Acceleration varies with time and becomes maximum when the particle is at rest."
- This is correct. The acceleration is maximum at the extreme positions when the particle is momentarily at rest.
- The correct statement regarding the particle executing SHM is Option 4: "Acceleration varies with time and becomes maximum when the particle is at rest."
Topper's Solved these Questions
Similar Questions
A particle is executing S.H.M. along a straight line. The graph showing the variation of kinetic, potential and total energy K, U and T respectively with displacement is -

View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line
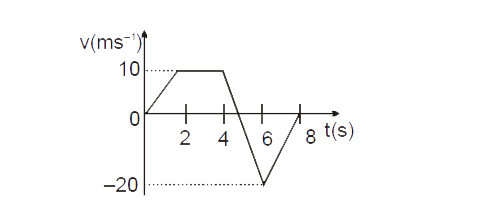
Choose the incorrect statement. The particle comes to rest at
View Solution
Knowledge Check
A particle is executing S.H.M. along a straight line. The graph showing the variation of kinetic, potential and total energy K, U and T respectively with displacement is -
 A
A B
B C
C D
D
A particle is moving along a straight line.
AIf the acceleration of the particle is more than that of another object, the particle is moving faster.BIf the acceleration is positive, the speed must be increasing.CIf the acceleration and the velocity have the same sign, the speed must be increasing.DIf the acceleration is zero, the velocity is constant but the speed may be changing.The figure shows a velocity-time graph of a particle moving along a straight line
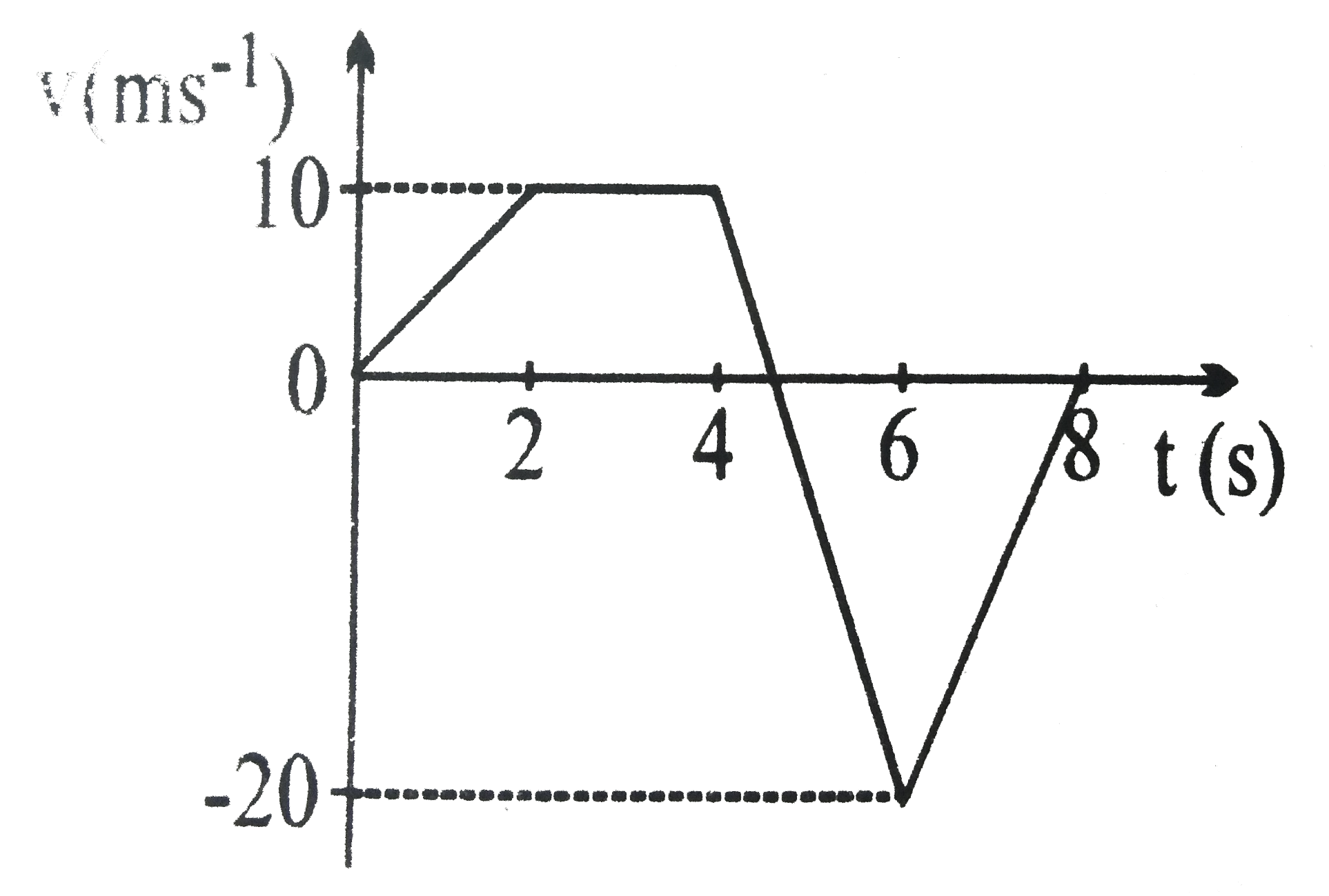
Choose the incorrect statement. The particle comes to rest atAt=0sBt=5sCt=8sDnoe of these
Displacement versus time curve for a particle executing SHM is shown in figure. Choose the correct statements.

View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionDisplacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements

View SolutionThe displacment versus timecurves for a particle executing SHM is show in figure . Choose the correct statement (s)
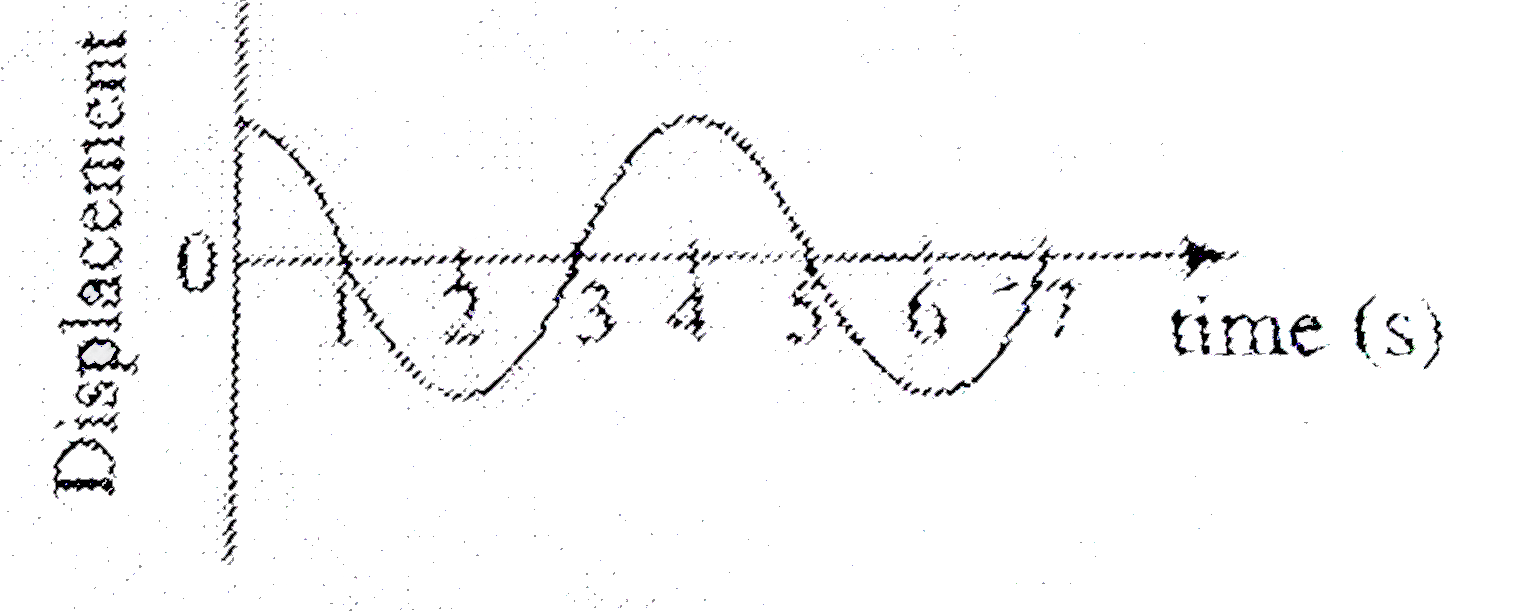
View SolutionThe figure shows velocity-time graph of a particle moving along a straight line. Identify the correct statement.
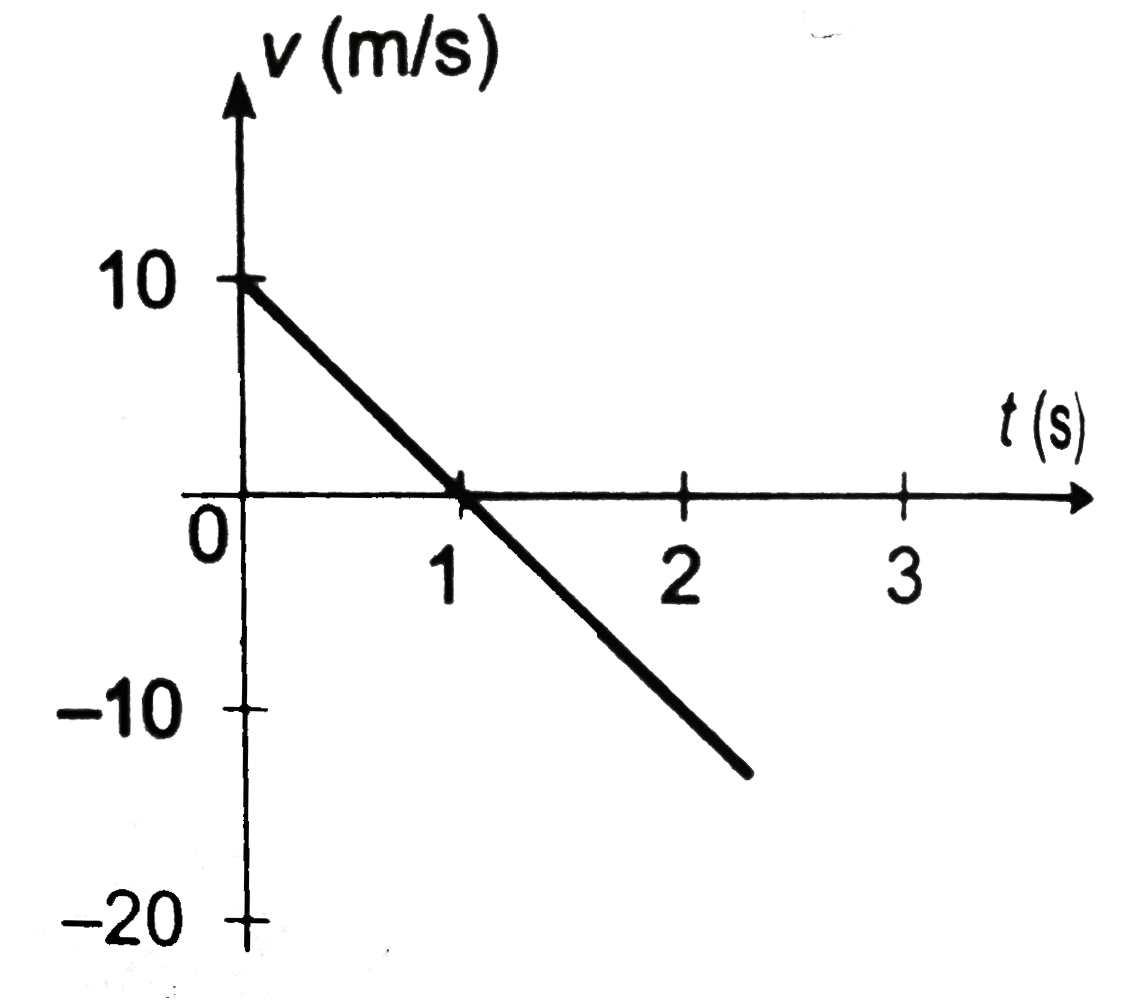
View Solution
