The ratio of vms:vmp:vavg is (Symbols have their usual meaning )
√3:√2:√π8
√3:√2:√83
√3:√8π:√2
√3:√2:√8π
To solve the problem of finding the ratio of vms:vmp:vavg, we will first define each of the velocities involved:
1. Mean Square Velocity (vms):
vms=√3RTM
2. Maximum Possible Speed (vmp):
vmp=√2RTM
3. Average Velocity (vavg):
vavg=√8RTπM
Now, we will express the ratio vms:vmp:vavg.
Step 1: Write the expressions for each velocity
- vms=√3RTM
- vmp=√2RTM
- vavg=√8RTπM
Step 2: Factor out common terms
Since all three velocities have the term √RTM in common, we can factor it out:
vms:vmp:vavg=√3:√2:√8π
Step 3: Simplify the ratio
To simplify the ratio, we can express it in terms of a common denominator. We will use the values of √3, √2, and √8π to find a numerical ratio.
- Let’s calculate √3, √2, and √8π:
- √3≈1.732
- √2≈1.414
- √8π≈√83.14≈1.595
Step 4: Convert to a numerical ratio
Now we can express the ratio numerically:
vms:vmp:vavg≈1.732:1.414:1.595
Step 5: Normalize the ratio
To express this in a simpler form, we can divide each term by the smallest value (which is √2):
1.7321.414:1.4141.414:1.5951.414≈1.224:1:1.127
Final Ratio
Thus, the final ratio vms:vmp:vavg can be approximated as:
√3:√2:√8πor approximately1.224:1:1.127
Summary
The ratio of vms:vmp:vavg is approximately √3:√2:√8π.
vms=√3RTM
vmp=√2RTM
vavg=√8RTπM
- vms=√3RTM
- vmp=√2RTM
- vavg=√8RTπM
Since all three velocities have the term √RTM in common, we can factor it out:
vms:vmp:vavg=√3:√2:√8π
To simplify the ratio, we can express it in terms of a common denominator. We will use the values of √3, √2, and √8π to find a numerical ratio.
- √3≈1.732
- √2≈1.414
- √8π≈√83.14≈1.595
Now we can express the ratio numerically:
vms:vmp:vavg≈1.732:1.414:1.595
To express this in a simpler form, we can divide each term by the smallest value (which is √2):
1.7321.414:1.4141.414:1.5951.414≈1.224:1:1.127
Thus, the final ratio vms:vmp:vavg can be approximated as:
√3:√2:√8πor approximately1.224:1:1.127
The ratio of vms:vmp:vavg is approximately √3:√2:√8π.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Bohr magnetonis given by (symbols have their usual meanings)
A4πmeeh2B4πmeehCeh24πmeDeh4πmeThe correct combination is (symbols have their usual meanings)
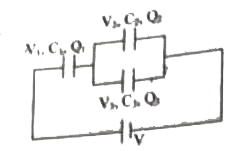 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3The correct form of Stroke's law is (symbols have their usual meanings)
A→F=−6πηa→vB→F=6πηa→vC→F=−4πηa→vD→F=4πηa→v
(a) Explain the meaning of the following equation of motion :
v=u+at
where symbols have their usual meanings.
(b) A body starting from rest travels with uniform acceleration. If it travels 100 m in 5 s, what is the value of acceleration.
View SolutionUse velocity time graph to derive the relation : v2−u2=2 as, where the symbols have their usual meaning.
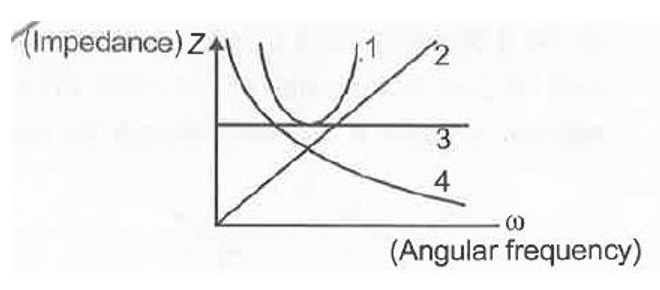
View SolutionChoose the correct combination for the given graph.
(Symbols have their usual meaning)
View SolutionWhich of the following is correct ? (symbols have their ususal meanings)
View SolutionThe dispersive power (w) of the material of a prism is (where symbols have their usual meanings)
View Solution
