The rotational inertia of a disc about its geometrical axis does not depend upon its
Diameter
Distribution of mass
Mass
Speed of rotation
To solve the question regarding the rotational inertia of a disc about its geometrical axis, we need to understand the factors that influence it.
1. Understanding Rotational Inertia:
Rotational inertia, also known as the moment of inertia (I), is a measure of an object's resistance to changes in its rotation. For a disc, it is calculated based on its mass distribution relative to the axis of rotation.
2. Formula for Moment of Inertia of a Disc:
The moment of inertia (I) of a uniform disc about its geometrical axis is given by the formula:
I=12MR2
where M is the mass of the disc and R is the radius of the disc.
3. Factors Affecting Moment of Inertia:
From the formula, we can see that the moment of inertia depends on:
- The mass (M) of the disc.
- The radius (R) of the disc.
4. Identifying the Non-Dependent Factor:
The question asks what the rotational inertia does not depend on. From our analysis, we see that:
- It does not depend on the speed of rotation. The speed of rotation affects the angular velocity but does not change the moment of inertia itself.
- It also does not depend on the material of the disc, as long as the mass and radius remain constant.
5. Conclusion:
Therefore, the rotational inertia of a disc about its geometrical axis does not depend upon its speed of rotation.
Final Answer:
The rotational inertia of a disc about its geometrical axis does not depend upon its speed of rotation.
Rotational inertia, also known as the moment of inertia (I), is a measure of an object's resistance to changes in its rotation. For a disc, it is calculated based on its mass distribution relative to the axis of rotation.
The moment of inertia (I) of a uniform disc about its geometrical axis is given by the formula:
I=12MR2
where M is the mass of the disc and R is the radius of the disc.
From the formula, we can see that the moment of inertia depends on:
- The mass (M) of the disc.
- The radius (R) of the disc.
The question asks what the rotational inertia does not depend on. From our analysis, we see that:
- It does not depend on the speed of rotation. The speed of rotation affects the angular velocity but does not change the moment of inertia itself.
- It also does not depend on the material of the disc, as long as the mass and radius remain constant.
Therefore, the rotational inertia of a disc about its geometrical axis does not depend upon its speed of rotation.
The rotational inertia of a disc about its geometrical axis does not depend upon its speed of rotation.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
A1 IBI/2CIDI/4The moment of inertia of a body about a given axis of rotation depends upon :-
Athe distribution of massBdistance of particle of body from the axis of rotationCshape of the bodyDall of the above2Two thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
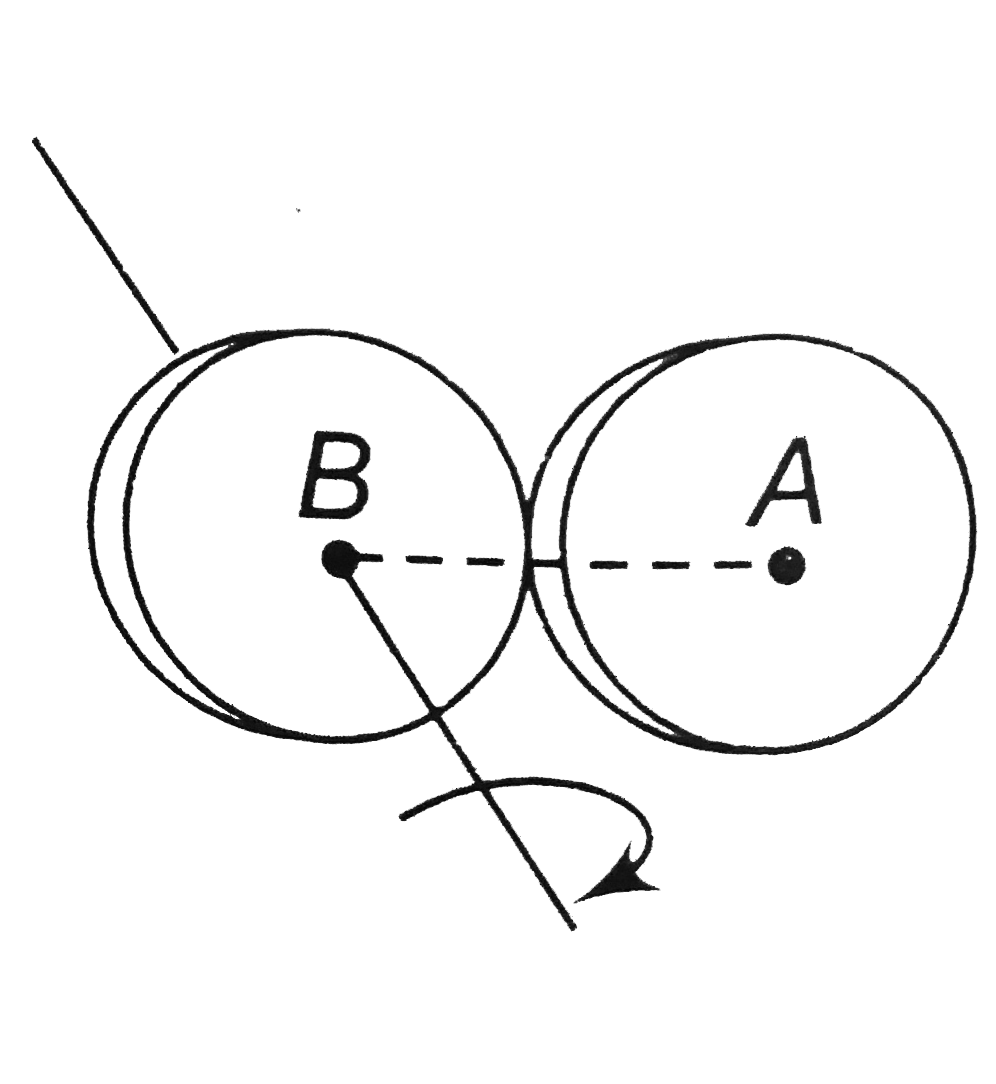 .A2Mr2B3Mr2C4Mr2D5Mr2
.A2Mr2B3Mr2C4Mr2D5Mr2
The moment of inertia of a disc about an axis through its centre and perpendicular to its plane is 12MR2 . Its moment of inertia about any diameter will be __________
View SolutionMoment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is 12MR2. Determine the moment of inertia of this disc about its diameter and about a tangent perpendicular to its plane.
View SolutionTwo thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
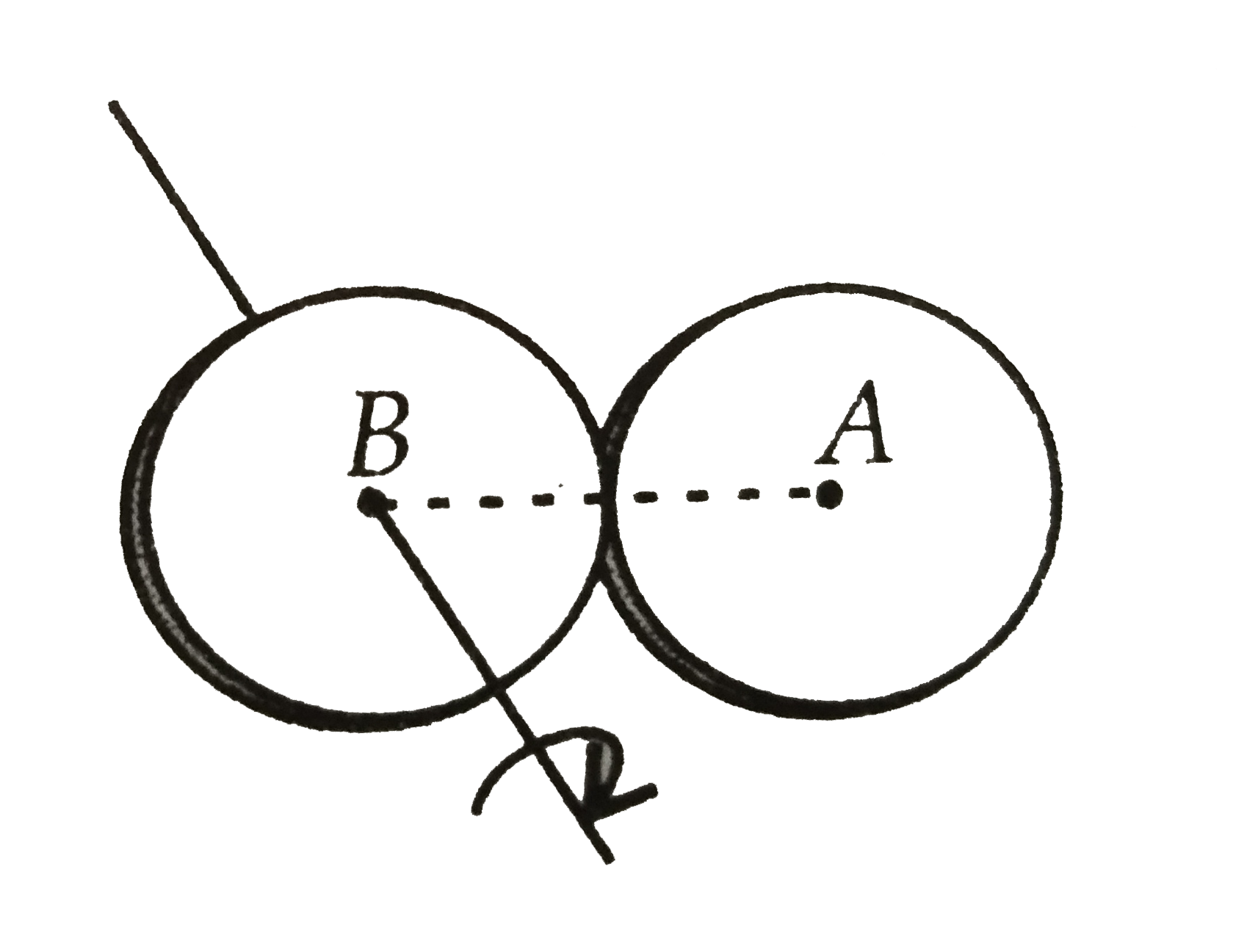
View SolutionThe moment of inertia of a disc of radius 0.5m about its geometric axis is 2kg-m2 . If a string is tied to its circumference and a force of 10 Newton is applied, the value of torque with respect to this axis will be:
View SolutionA circular disc is to be made by using equal masses of aluminium and iron. To get maximum moment of inertia, about its geometrical axis, it should be so prepared that
View Solution
