A force with a given magnitude is to be applied to a wheel. The torque can be maximised by
Applying the force near the axle, radially outward from the axle
Applying the force near the rim, radially outward from the axle
Applying the force near the axle, parallel to a tangent to the wheel
Applying the force at the rim, tangent to the rim
To maximize the torque applied to a wheel with a given force, we can follow these steps:
Step 1: Understand the Torque Formula
The torque (τ) produced by a force (F) applied at a distance (R) from the pivot point is given by the formula:
τ=R⋅F⋅sin(θ)
where:
- τ is the torque,
- R is the distance from the pivot point to the point where the force is applied,
- F is the magnitude of the force,
- θ is the angle between the radius vector (R) and the force vector (F).
Step 2: Maximize the Distance (R)
To maximize torque, we want R to be as large as possible. In the case of a wheel, R is the radius of the wheel. Thus, applying the force at the edge of the wheel maximizes R.
Step 3: Maximize the Angle (θ)
The sine function reaches its maximum value of 1 when the angle θ is 90 degrees. Therefore, to maximize torque, we need to apply the force such that it is perpendicular to the radius vector.
Step 4: Apply the Force Tangentially
To achieve both maximum R and maximum θ, the force should be applied tangentially to the wheel. This means that the force should be directed along the tangent line at the point of application on the wheel's rim.
Conclusion
By applying the force tangentially at the rim of the wheel, we ensure that:
- R is maximized (equal to the radius of the wheel),
- θ is maximized (equal to 90 degrees).
Thus, the torque is maximized when the force is applied tangentially to the rim of the wheel.
Final Answer
The torque can be maximized by applying the force tangentially at the rim of the wheel.
---
The torque (τ) produced by a force (F) applied at a distance (R) from the pivot point is given by the formula:
τ=R⋅F⋅sin(θ)
where:
- τ is the torque,
- R is the distance from the pivot point to the point where the force is applied,
- F is the magnitude of the force,
- θ is the angle between the radius vector (R) and the force vector (F).
To maximize torque, we want R to be as large as possible. In the case of a wheel, R is the radius of the wheel. Thus, applying the force at the edge of the wheel maximizes R.
The sine function reaches its maximum value of 1 when the angle θ is 90 degrees. Therefore, to maximize torque, we need to apply the force such that it is perpendicular to the radius vector.
To achieve both maximum R and maximum θ, the force should be applied tangentially to the wheel. This means that the force should be directed along the tangent line at the point of application on the wheel's rim.
By applying the force tangentially at the rim of the wheel, we ensure that:
- R is maximized (equal to the radius of the wheel),
- θ is maximized (equal to 90 degrees).
The torque can be maximized by applying the force tangentially at the rim of the wheel.
Topper's Solved these Questions
Similar Questions
For shown situation, what will be the magnitude of minimum force in newton that can be applied in any direction so that the resultant force is along east direction?

View SolutionA wheel of radius 20 cm has forces applied to it as shown in the figure. The torque produced by the forces 4N at A, 8N at B, 6N at C, and 9N at D at angles indicated is :

View Solution
Knowledge Check
Torque can NOT be given by
Aproduct of magnitude of the force and lever arm of the force.Bproduct of magnitude of the force and perpendicular distance between its line of action of the force.Cproduct of magnitude of force and moment arm of the force.Dproduct of magnitude of the force and maximum distance covered.Four forces of the same magnitude act on a square as shown in figure. The square can rotate about point O, mid point of one of the edges. The force which can produce greatest torque is
 AF1BF2CF3DF4
AF1BF2CF3DF4Two forces, one with a magnitude of 3N and the other with a magnitude of 5N ,are applied to an object. For which orientations of the forces shown in the diagrams is the magnitude of the acceleration of the object the least ?
A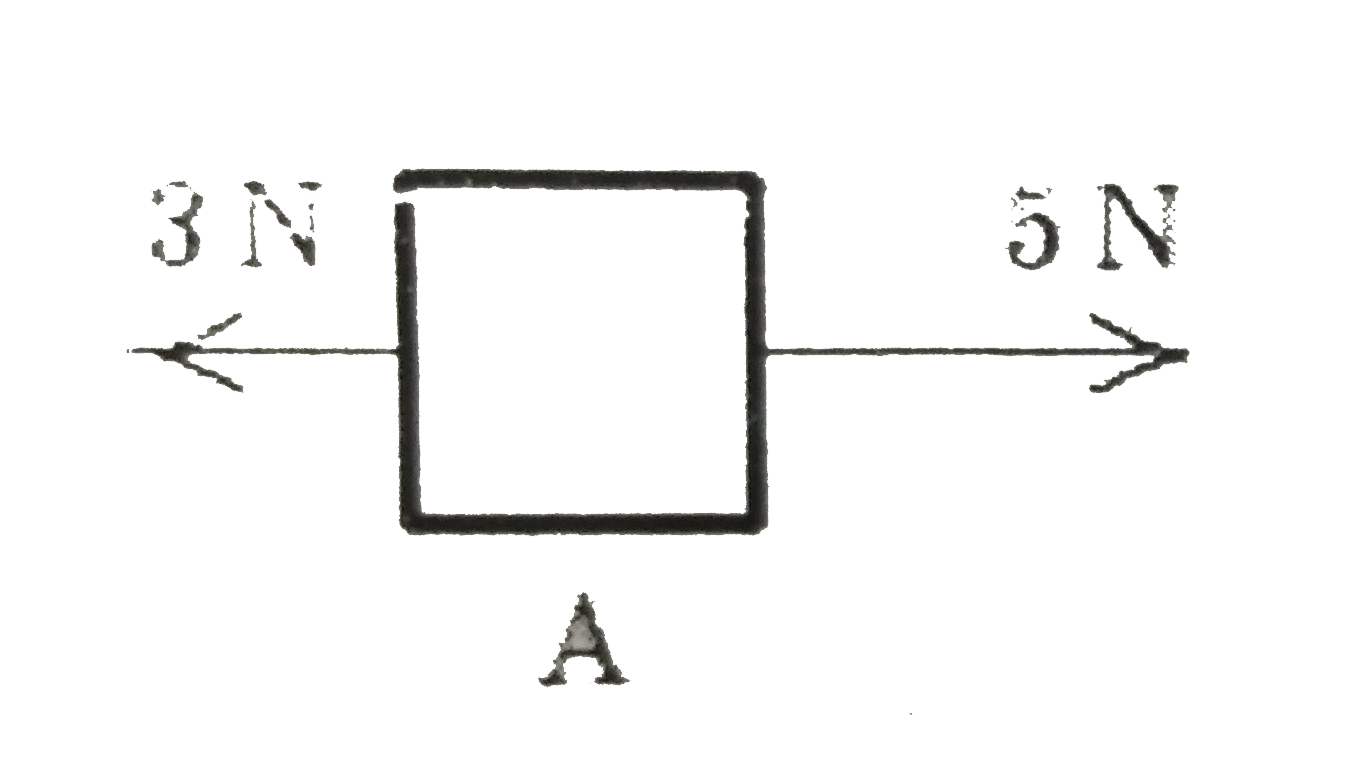 B
B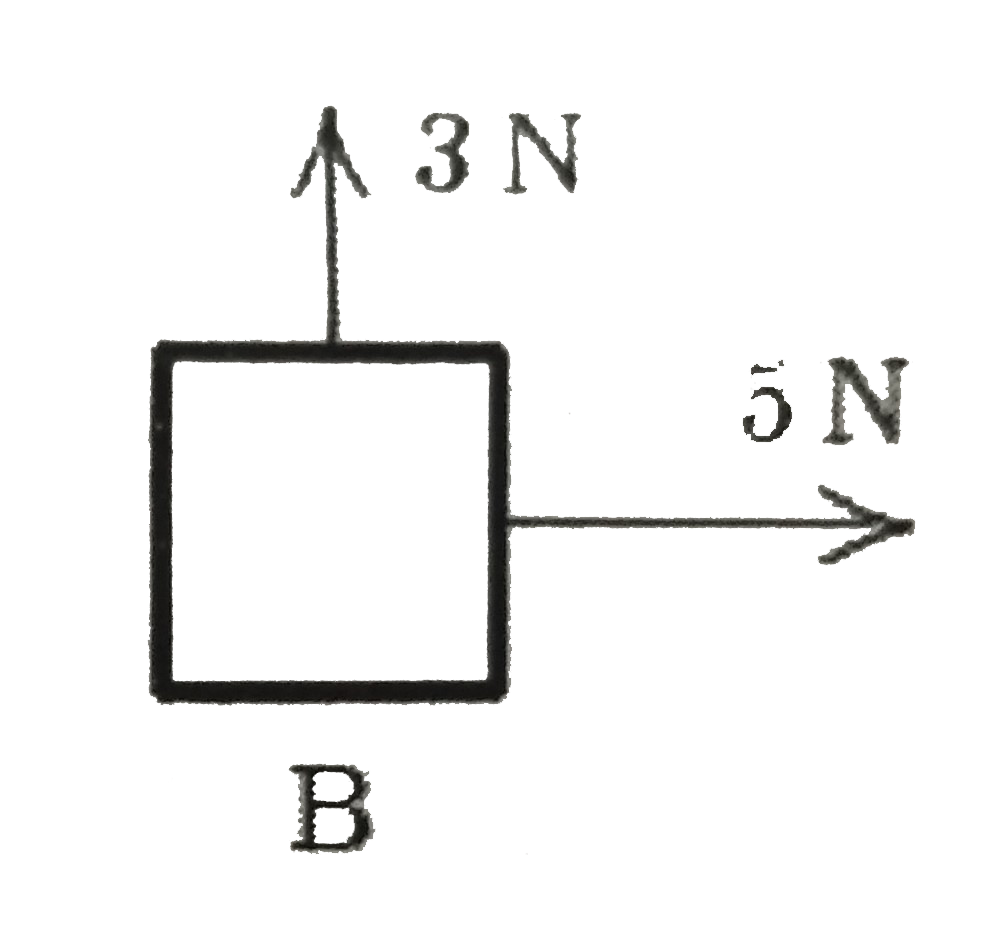 C
C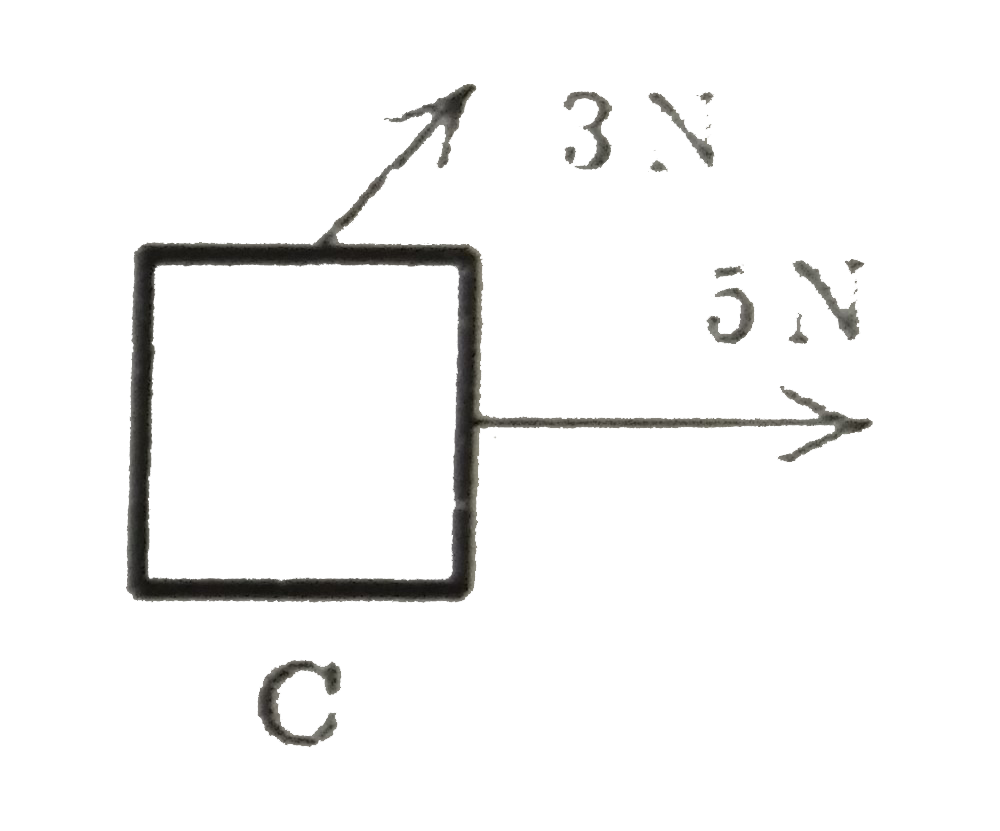 D
D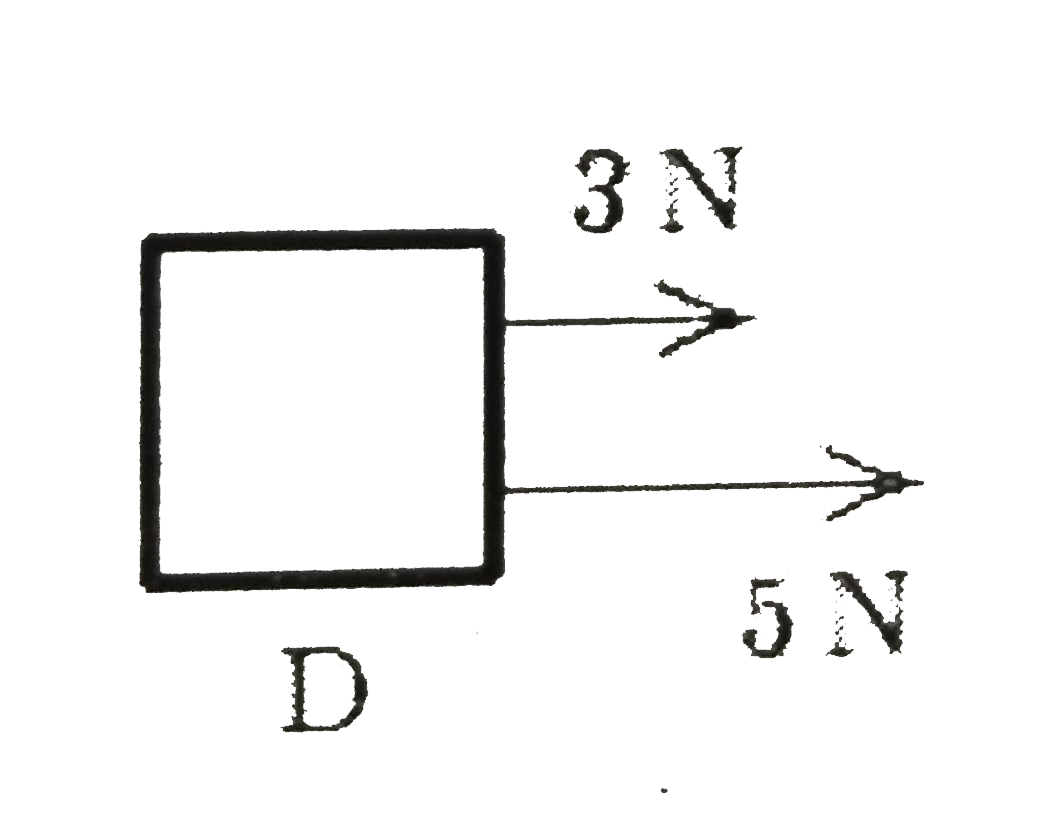
When a constant torque is applied on a rigid body, then
View SolutionOne end of meter stick is pinned to a table to that stick can rotate freely in aplane parallel to the table surface. Two horizontal forces are applied to the stick such that the rod does not rotate at all. One force has a magnitude of 2N and is applied perpendicular to the stick at the free end. The other force has a magnitude of 8N and acts at 30∘ with respect in the length of the stick. At what distance from the pinned end is the 8N force applied.
View SolutionA force of 100N is applied tangentially to the rim of a wheel of diameter 120 cm. The wheel rotates about an axis passing through its centre. What is the torque acting on the wheel?
View SolutionThe figure shows the top view of a door that is 2 m wide. Two forces are applied to the door as indicated. What is the magnitude of the net torque on the door with respect to the hinge?
View SolutionA wheel of radius R has an axle of radius R/5. A force F is applied tangentially to the wheel. To keep the system in a state of "rotational" rest, a force F' is applied tangentially to the axle. The value of F' is
View Solution
