The ends of metal road are maintained at temperature 120°C and 150°C. The rate of heat flow in the road is to be found to be 10Js. If an identical rod is connected in parallel with this rod and ends temperature are maintained at 220°C and 250°C, then net rate of flow of heat will be
10Js
20 J/s
30 J/s
15 J/s
To solve the problem, we need to analyze the heat flow through two identical rods connected in parallel, with different temperature differences.
1. Identify the Given Values:
- For the first rod:
- Temperature difference (ΔT₁) = 150°C - 120°C = 30°C
- Rate of heat flow (H₁) = 10 J/s
- For the second rod:
- Temperature difference (ΔT₂) = 250°C - 220°C = 30°C
2. Understand the Heat Flow Relationship:
- The rate of heat flow (H) through a rod is given by the formula:
H=ΔTR
where R is the thermal resistance of the rod. Since both rods are identical, they will have the same thermal resistance (R).
3. Calculate Heat Flow for Each Rod:
- For the first rod:
H₁=ΔT₁R=30°CR
Given that H₁ = 10 J/s, we can express this as:
10=30R⟹R=3010=3(units of resistance)
4. Calculate Heat Flow for the Second Rod:
- For the second rod:
H₂=ΔT₂R=30°CR
Since R is the same, we can substitute R:
H₂=303=10J/s
5. Combine the Heat Flows:
- Since the rods are connected in parallel, the total heat flow (H_total) is the sum of the heat flows through each rod:
Htotal=H₁+H₂=10J/s+10J/s=20J/s
Final Answer:
The net rate of flow of heat when an identical rod is connected in parallel is 20 J/s.
---
- For the first rod:
- Temperature difference (ΔT₁) = 150°C - 120°C = 30°C
- Rate of heat flow (H₁) = 10 J/s
- For the second rod:
- Temperature difference (ΔT₂) = 250°C - 220°C = 30°C
- The rate of heat flow (H) through a rod is given by the formula:
H=ΔTR
where R is the thermal resistance of the rod. Since both rods are identical, they will have the same thermal resistance (R).
- For the first rod:
H₁=ΔT₁R=30°CR
Given that H₁ = 10 J/s, we can express this as:
10=30R⟹R=3010=3(units of resistance)
- For the second rod:
H₂=ΔT₂R=30°CR
Since R is the same, we can substitute R:
H₂=303=10J/s
- Since the rods are connected in parallel, the total heat flow (H_total) is the sum of the heat flows through each rod:
Htotal=H₁+H₂=10J/s+10J/s=20J/s
The net rate of flow of heat when an identical rod is connected in parallel is 20 J/s.
Topper's Solved these Questions
Similar Questions
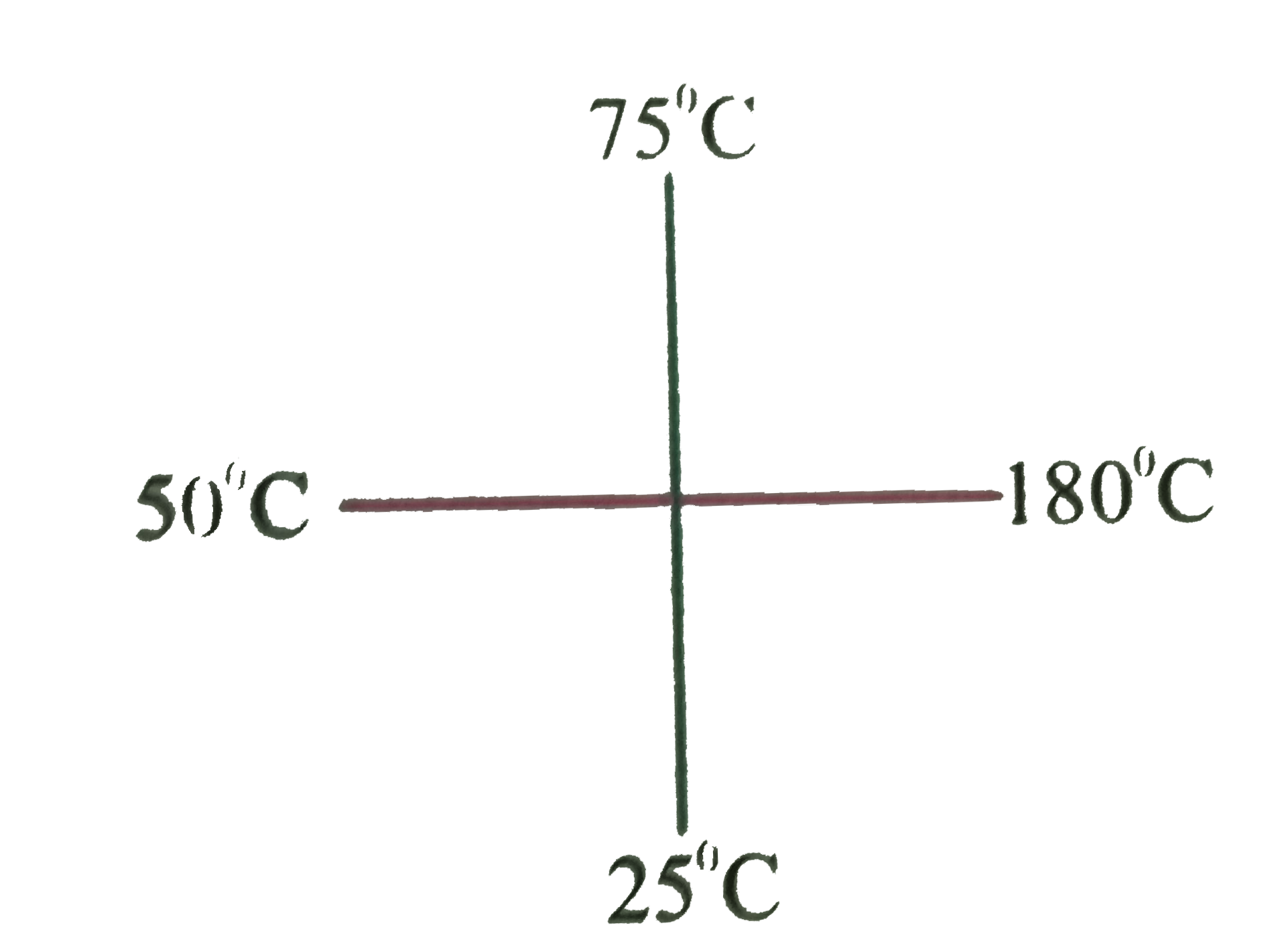
Two identical rods are joined at their middle points The ends are maintained at constant temperatures as indicated Find the temperature of the junction
 .
.
View SolutionThe two ends of a metal rod are maintained at temperatures 100∘C and 110∘C . The rate of heat flow in the rod is found to be 4.0j/s. If the ends are maintaind at temperatures 200∘C and 210∘C, the rate of heat flow will be :
View Solution
Knowledge Check
The two ends of a metal rod are maintained at temperature 100∘C and 110∘C. The rate of heat flow in the rod is found to be 4.0J/s. If the ends are maintained at temperature s 200∘C and 210∘C. The rate of heat flow will be
A44.0J/sB16.8J/sC8.0J/sD4.0J/sThe two ends of a metal rod are maintained at temperatures 100∘C and 110∘C. The rate of heat flow in the rod is found to be 4.0 J/s. If the ends are now maintained at temperatures 200∘C and 210∘C, the rate of flow of heat will be
A16.8 j/sB8.0 J/sC4.0 J/sD44.8 J/sThe two ends of a metal rod are maintained at temperatures 100∘C and 110∘C . The rate of heat flow in the rod is found to be 4.0j/s. If the ends are maintaind at temperatures 200∘C and 210∘C, the rate of heat flow will be :
A16.8j/sB8.0j/sC4.0j/sD44.0j/s
The ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View SolutionFive identical rods are joined as shown in figure. Point A and C are maintained at temperature 120°C and 20°C respectively. The temperature of junction B will be

View SolutionOne end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View SolutionThe ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
View SolutionRates of emission of heat by perfectly black body maintained at temperatures 27° C and 927° Care in ratio
View Solution
