A ball of mass m by means of two massless strings of equal length l is connected to a vertical rotating rod. The strings are tied to rod with a separation l. For what angular speed off the rod, lower string just becomes taut?
To solve the problem of determining the angular speed ω at which the lower string of a ball becomes taut, we can follow these steps:
Step 1: Understand the Setup
We have a ball of mass m connected to a vertical rotating rod by two massless strings of equal length l. The strings are tied to the rod with a separation of l. The upper string will become taut before the lower string does as the rod rotates.
Hint: Visualize the setup and identify the forces acting on the ball.
Step 2: Analyze Forces Acting on the Ball
When the lower string just becomes taut, the tension in the lower string T2 is zero. The forces acting on the ball are:
- The weight of the ball mg acting downwards.
- The tension T1 in the upper string acting at an angle.
Hint: Draw a free-body diagram to identify the forces and their components.
Step 3: Set Up the Equations
For vertical equilibrium, when the lower string is just taut:
T1sin(30∘)=mg
For horizontal equilibrium (centripetal force), we have:
T1cos(30∘)=mω2R
Where R is the horizontal distance from the axis of rotation to the ball.
Hint: Remember that sin(30∘)=12 and cos(30∘)=√32.
Step 4: Find the Radius R
The radius R can be expressed in terms of the length of the string and the angle:
R=lcos(30∘)=l⋅√32
Hint: Substitute the value of cos(30∘) into the equation for R.
Step 5: Substitute R into the Equations
Substituting R into the horizontal equilibrium equation:
T1cos(30∘)=mω2(l⋅√32)
Hint: This will help you relate T1 to ω.
Step 6: Solve for T1
From the vertical equilibrium equation:
T1=2mg
Substituting this into the horizontal equation gives:
2mg⋅√32=mω2(l⋅√32)
Hint: Simplify the equation by canceling m and √32.
Step 7: Solve for ω
After simplification:
2g=ω2l
Rearranging gives:
ω2=2gl
Taking the square root:
ω=√2gl
Hint: Ensure you understand the relationship between angular speed and gravitational force.
Final Answer
The angular speed ω at which the lower string just becomes taut is:
ω=√2gl
We have a ball of mass m connected to a vertical rotating rod by two massless strings of equal length l. The strings are tied to the rod with a separation of l. The upper string will become taut before the lower string does as the rod rotates.
When the lower string just becomes taut, the tension in the lower string T2 is zero. The forces acting on the ball are:
- The weight of the ball mg acting downwards.
- The tension T1 in the upper string acting at an angle.
For vertical equilibrium, when the lower string is just taut:
T1sin(30∘)=mg
For horizontal equilibrium (centripetal force), we have:
T1cos(30∘)=mω2R
Where R is the horizontal distance from the axis of rotation to the ball.
The radius R can be expressed in terms of the length of the string and the angle:
R=lcos(30∘)=l⋅√32
Substituting R into the horizontal equilibrium equation:
T1cos(30∘)=mω2(l⋅√32)
From the vertical equilibrium equation:
T1=2mg
Substituting this into the horizontal equation gives:
2mg⋅√32=mω2(l⋅√32)
After simplification:
2g=ω2l
Rearranging gives:
ω2=2gl
Taking the square root:
ω=√2gl
The angular speed ω at which the lower string just becomes taut is:
ω=√2gl
Topper's Solved these Questions
Similar Questions
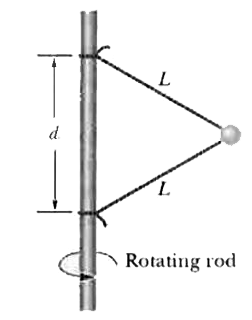
In fig 1.34 kg ball is connected by means of two mass less strings, each of length L=1.70m, to a vertical, rotating rod. The strings are tied to the rod with separation d=1.70 m and are taut. The tenion in the upper string is 35N. What are the (a) tension in the lower string, (b) magnitude of the net (b) magnitude of the net force →Fnet on the all, and (c) speed of the ball? (d) What is the direction of →Fnet?
View Solutiona ball of mass 240g is attached to the verticle rod by means of two strings. When the ball rotates about the axis of rod, the strings are extended as shown in the figure.
(a) find the angular speed of the ball if tension in lower string is 16N.
(b) What is tension in the upper string?

View Solution
Knowledge Check
A stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
ARadially outwardBRadialy inwardCTangentially outwardDWith acceleration mv2lA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√TmlA stone of mass m tied to a string of length l rotates along circumference of a circle with constant speed v. The torque on the stone is
AzeroBmv2×lCm2vlDmv2l
A particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
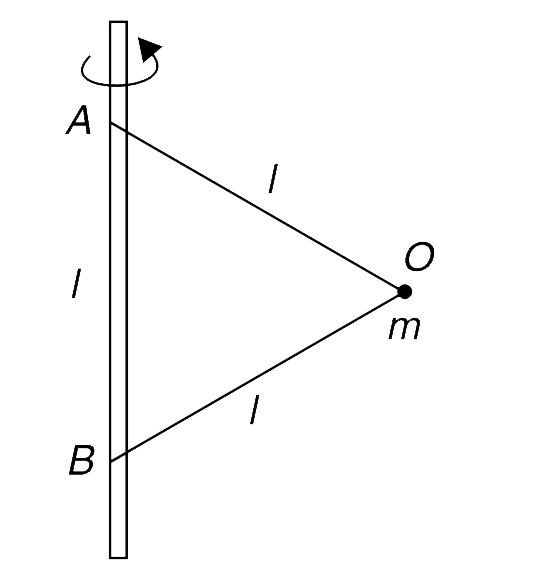
(a) Find the values of ω for which the particle remains at point B.
(b) Find the range of values of ω for which tension (T1) in the string AO is greater than mg but the other string remains slack
(c) Find the value of ω for which tension (T1) in string AO is twice the tension (T2) in string BO
(d) Assume that both strings are taut when the string AO breaks. What will be nature of path of the particle moment after AO breaks ?
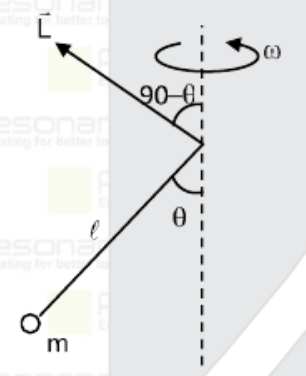
View SolutionA bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .
.
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
View Solution