Consider a system of two identical particles. One of the particle is at rest and other has an acceleration →a. The centre of mass has an acceleration
zero
12a
→a
2→a
The correct Answer is:B
To solve the problem of finding the acceleration of the center of mass of a system of two identical particles, we can follow these steps:
Step 1: Define the system
We have two identical particles, each with mass m. One particle is at rest, and the other particle has an acceleration →a.
Step 2: Identify the accelerations of the particles
Let:
- Particle 1 (at rest): →a1=0
- Particle 2 (accelerating): →a2=→a
Step 3: Write the formula for the acceleration of the center of mass
The acceleration of the center of mass →acm for a system of particles is given by the formula:
→acm=∑mi→ai∑mi
where mi is the mass of the i-th particle and →ai is its acceleration.
Step 4: Substitute the values into the formula
In our case, we have:
- For Particle 1: m1=m and →a1=0
- For Particle 2: m2=m and →a2=→a
Substituting these values into the formula gives:
→acm=m⋅0+m⋅→am+m
Step 5: Simplify the expression
This simplifies to:
→acm=0+m→a2m=m→a2m=→a2
Step 6: Conclusion
Thus, the acceleration of the center of mass is:
→acm=→a2
Final Answer
The acceleration of the center of mass is →a2.
---
We have two identical particles, each with mass m. One particle is at rest, and the other particle has an acceleration →a.
Let:
- Particle 1 (at rest): →a1=0
- Particle 2 (accelerating): →a2=→a
The acceleration of the center of mass →acm for a system of particles is given by the formula:
In our case, we have:
- For Particle 1: m1=m and →a1=0
- For Particle 2: m2=m and →a2=→a
This simplifies to:
Thus, the acceleration of the center of mass is:
The acceleration of the center of mass is →a2.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)2videos
COLLISION
- BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II20videos
COLLISION
- BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II17videos
COLLISION
- BOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE1videos
AC CIRCUITS
- BOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -43videos
CURRENT ELECTRICITY
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider a system of two identical particles. One of the particls is at rest and the other has an acceleration.The centre of mass has an acceleration vaca The centre of mass has an acceleration.
AzeroB12→aC→aD2→a - Question 2 - Select One
Consider a system of two identical particles. One of the particle is at rest and other has an acceleration →a. The centre of mass has an acceleration
A2aBa/2CaD2a2 - Question 3 - Select One
There are two particles of same mass. If one of the particles is at rest always and the other has an acceleration →a. Acceleration of centre of mass is?
AZeroB12→aC→aDcentre of mass for such a system can not be defined.
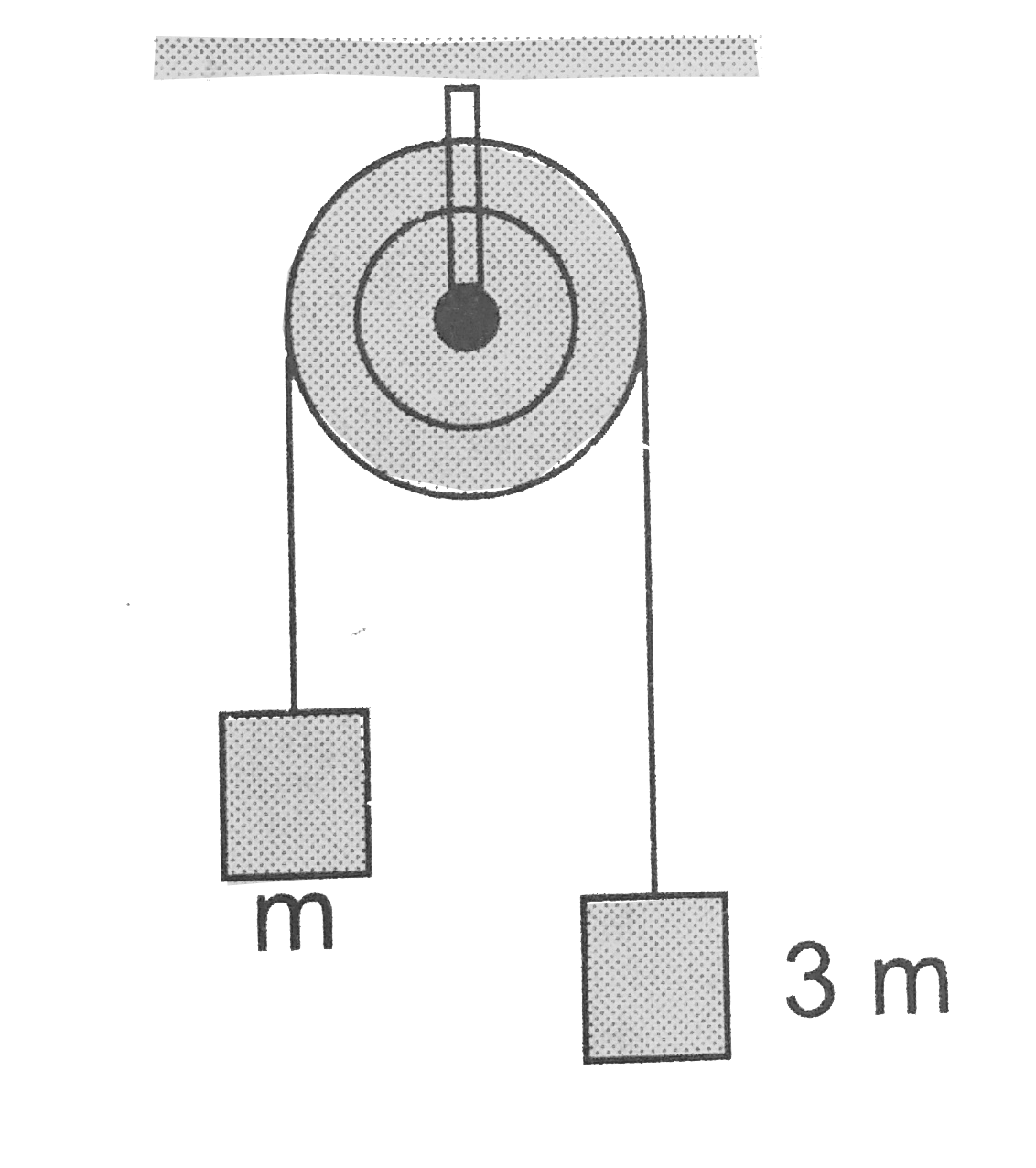
If the system is released, then the acceleration of the centre of mass of the system is :
 .View Solution
.View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionThe magnitude of acceleration of centre of mass of the system is
 View Solution
View SolutionConsider a system of two particles having masses 2kg and 5 kg the particle of mass 2 kg is pushed towards the centre of mass of particles through a distance 5 m,by what distance would particle of mass 5kg move so as to keep the centre of mass of particles at the original position?
View Solution