If gas expands according to relation P = 4 V, then work done in expansion Vo to 3Vo
72V2o
18V2o
16V2o
48V2o
To find the work done during the expansion of a gas from volume V0 to 3V0 given the relation P=4V, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W during an expansion can be calculated using the formula:
W=∫V2V1PdV
where P is the pressure and V1 and V2 are the initial and final volumes, respectively.
Step 2: Substitute the Pressure Relation
Given the relation P=4V, we substitute this into the work done formula:
W=∫3V0V04VdV
Step 3: Integrate the Function
Now, we need to integrate 4V:
W=4∫3V0V0VdV
The integral of V is:
∫VdV=V22
So, we have:
W=4(V22)3V0V0
Step 4: Evaluate the Integral
Now we evaluate the integral from V0 to 3V0:
W=4((3V0)22−(V0)22)
Calculating the squares:
W=4(9V202−V202)
W=4(9V20−V202)
W=4(8V202)
W=4⋅4V20
W=16V20
Final Answer
The work done in the expansion from V0 to 3V0 is:
W=16V20
The work done W during an expansion can be calculated using the formula:
W=∫V2V1PdV
where P is the pressure and V1 and V2 are the initial and final volumes, respectively.
Given the relation P=4V, we substitute this into the work done formula:
W=∫3V0V04VdV
Now, we need to integrate 4V:
W=4∫3V0V0VdV
The integral of V is:
∫VdV=V22
So, we have:
W=4(V22)3V0V0
Now we evaluate the integral from V0 to 3V0:
W=4((3V0)22−(V0)22)
Calculating the squares:
W=4(9V202−V202)
W=4(9V20−V202)
W=4(8V202)
W=4⋅4V20
W=16V20
The work done in the expansion from V0 to 3V0 is:
W=16V20
Topper's Solved these Questions
Similar Questions
An ideal gas whose adiabatic exponent is gamma is expanded according to the relation P=αV .The molar specific heat of the process is (alpha is a positive constant)
View SolutionAn ideal gas has adiabatic exponenty. It expands according to the law P=αV, where is αconstant. For this process, the Bulk modulus of the gas is
View Solution
Knowledge Check
One mole of an ideal gas at temperature T1 expands according to the law (P/V) = constant. Find the work done when the final temperature becomes T2.
AR(T2−T1)B(R/2)(T2−T1)C(R/4)(T2−T1)DPV(T2−T1)A gas expands with temperature according to the relation V=KT23.Work done when the temperature changes by 60K is.
A10RB30RC40RD20RAn ideal gas expands according to the law P2V = constant . The internal energy of the gas
AIncreases continuouslyBDecreases continuouslyCRemain constantDFirst increases and then decreases
A gas undergoes expansion according to the following graph. Calculate work done by the gas
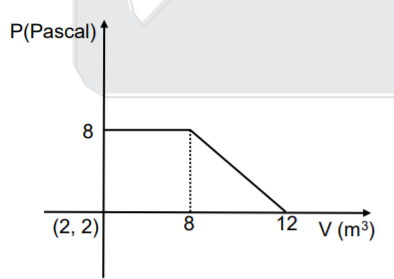
View SolutionOne mole of a gas expands obeying the relation as shown in the P/V diagram. The maximum temperature in this process is equal to
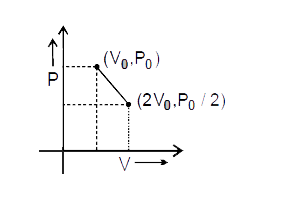
View SolutionA gas expands with temperature according to the relation V=KT2/3 where K is a constant. The work done by the gas when the temperature changes by 60 K is
View SolutionTwo moles of an ideal monoatomic gas at 27∘Coccupies a volume of V . If the gas is expanded adiabatically to the volume , 2V then the work done by the gas will be [λ=5/3,R=8.31j/molK]
View SolutionThe work done in increasing the potential of a capacitor from V volt to 2V volt is W Then, the work done in increasing the potential of the same capacitor from 2V volt to 4V volt will be.
View Solution
