Magnetic in a region is given by →B=B0ˆi+B0ˆj . Torque on a circular loop x2+z2=r2 carrying current i in anticlockwise direction as seen from a point on positive y-axis is
iπr²B0ˆk
–iπr²B0ˆk
iπr²ˆk
–iπrB0ˆk
To solve the problem of finding the torque on a circular loop carrying current in a magnetic field, we can follow these steps:
Step 1: Understand the Magnetic Field and Loop
The magnetic field is given by:
→B=B0^i+B0^j
This means the magnetic field has components in both the x and y directions.
The circular loop is defined by the equation:
x2+z2=r2
This indicates a circular loop in the x-z plane with radius r.
Step 2: Determine the Magnetic Moment
The magnetic moment →M of the loop can be calculated using the formula:
→M=I⋅A⋅^n
where I is the current, A is the area of the loop, and ^n is the unit vector normal to the plane of the loop.
The area A of the circular loop is:
A=πr2
Since the current is flowing anticlockwise when viewed from the positive y-axis, the unit normal vector ^n will be in the negative y-direction:
^n=−^j
Thus, the magnetic moment becomes:
→M=I⋅πr2⋅(−^j)=−πr2I^j
Step 3: Calculate the Torque
The torque →τ on the loop in a magnetic field is given by the cross product:
→τ=→M×→B
Substituting the values of →M and →B:
→τ=(−πr2I^j)×(B0^i+B0^j)
Step 4: Expand the Cross Product
Using the distributive property of the cross product:
→τ=−πr2I(^j×B0^i+^j×B0^j)
Since ^j×^j=0, we only need to calculate ^j×^i:
^j×^i=−^k
Thus, we have:
→τ=−πr2IB0(−^k)=πr2IB0^k
Step 5: Final Result
The torque on the circular loop is:
→τ=πr2B0I^k
Summary
The torque on the circular loop carrying current I in the magnetic field →B=B0^i+B0^j is given by:
→τ=πr2B0I^k
The magnetic field is given by:
→B=B0^i+B0^j
This means the magnetic field has components in both the x and y directions.
x2+z2=r2
This indicates a circular loop in the x-z plane with radius r.
The magnetic moment →M of the loop can be calculated using the formula:
→M=I⋅A⋅^n
where I is the current, A is the area of the loop, and ^n is the unit vector normal to the plane of the loop.
A=πr2
Since the current is flowing anticlockwise when viewed from the positive y-axis, the unit normal vector ^n will be in the negative y-direction:
^n=−^j
Thus, the magnetic moment becomes:
→M=I⋅πr2⋅(−^j)=−πr2I^j
The torque →τ on the loop in a magnetic field is given by the cross product:
→τ=→M×→B
Substituting the values of →M and →B:
→τ=(−πr2I^j)×(B0^i+B0^j)
Using the distributive property of the cross product:
→τ=−πr2I(^j×B0^i+^j×B0^j)
Since ^j×^j=0, we only need to calculate ^j×^i:
^j×^i=−^k
Thus, we have:
→τ=−πr2IB0(−^k)=πr2IB0^k
The torque on the circular loop is:
→τ=πr2B0I^k
The torque on the circular loop carrying current I in the magnetic field →B=B0^i+B0^j is given by:
→τ=πr2B0I^k
Topper's Solved these Questions
Similar Questions
A particle of charge q>0 is moving at speed v in the +z direction through a region of uniform magnetic field. The magnetic force on the particle →F=F0(3ˆi+4ˆj), where F0 is a positive constant.
(a) Determine the components Bx,By and Bz or at least as many of the three components as is possible from the information given.
(b) If it is given in addition that the magnetic field has magnitude 6F0qv , determine the magnitude of Bz.
View SolutionA rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
View Solution
Knowledge Check
A uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
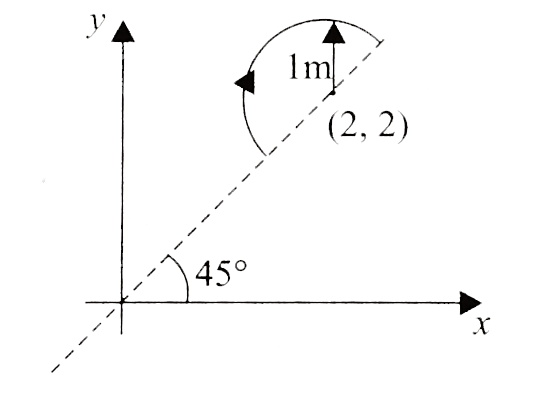 A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk)
A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk)The magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
Av0B0d2aBv0B0d3aCv0B0d22aD0A magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
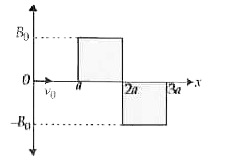
the magnetic field at x=a, The trajectory of the charge in this region can be like,A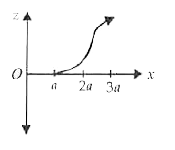 B
B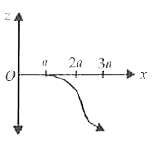 C
C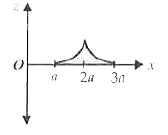 D
D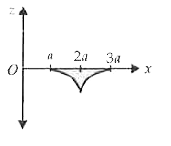
Given that →A=Axˆi+Ayˆj+Azˆk and →B=Bxˆi+Byˆj+Bzˆk. Find →A×→B
View SolutionFind the equation of the plane which contains the line of intersection of the planes:
→r.(ˆi−2ˆj+3ˆk)−4=0 and
→r.(−2ˆi+ˆj+ˆk)+5=0 and whose intercept on x-axis is equal to that of y-axis.
View SolutionIf →r=xˆi+yˆj+zˆk, then write the value of ∣∣→r׈i∣∣2.
View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like

View SolutionA magnet of magnetic moment of 50 ˆiAm2 is placed along the x - axis in magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the manet is
View Solution
