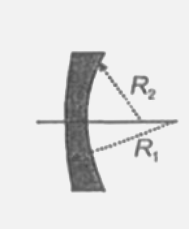
For convex lens, the radii of curvatures of the first and second surface are R1andR2 respectively. Using new Cartesian sign conventions they are Solution in Marathi
−R1,−R2
−R1,+R2
+R1,+R2
+R1,−R2
Step by step video & image solution for For convex lens, the radii of curvatures of the first and second surface are R_(1) and R_(2) respectively. Using new Cartesian sign conventions they are by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
When the force acting on the object and the velocity of the object both are along the same line, it is called ________
01:30View SolutionWhen image is fomred by reflaction, the field of veiw is maximum for
View SolutionOne surface of a lens is convex and the other is concave, if the radii of curvature are r_(1) and r_(2) respectively, the lens will be convex if
03:28View SolutionA biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
Assume that R1=R2,n1≠n3. The ratio, f1/f2, of the two focal lengths is equal to05:03View Solutionएक पतले लेंस के लिए फोकस दुरी का सूत्र अपवर्तनांक तथा वक्रता त्रिज्याओं के पदों में लिखिए! (अथवा) किसी उत्तल लेंस की फोकस दुरी f अपवर्तनांक n एवं लेंस की वक्रता त्रिज्याओं R1 व R2 के बिच सम्बन्ध लिखिए!
08:08View Solutionएक लेंस की सतहों की वक्रता - त्रिज्याओं का मान R1=+20cm तथा R2=+30cm हैं । लेंस के पदार्थ का अपवर्तनांक 1.6 हैं । इस लेंस की फोकस - दूरी निकालें यदि यह हवा में रखा हों
03:31View Solutionएक लेंस की सतहों की वक्रता - त्रिज्याओं का मान R1=+20cm तथा R2=+30cm हैं । लेंस के पदार्थ का अपवर्तनांक 1.6 हैं । इस लेंस की फोकस - दूरी निकालें यदि यह पानी (n = 1.33) में रखा हो ।
01:15View Solutionएक लेंस का एक पृष्ठ उत्तल है तथा दूसरा पृष्ठ अवतल है। यदि वक्रता त्रिज्याएँ क्रमश: r1 व r2 है, तब लेंस होगा। यदि
02:35View SolutionA double convex lens whose radii of curvature are R_(1) and R_(2) forms the image of a point object, placed on its axis. If the lens is revered, face to face, then the ratio of the distances of the images in the first and second case will be
01:13View SolutionFor convex lens, the radii of curvatures of the first and second surface are R1andR2 respectively. Using new Cartesian sign conventions they are
02:13View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can
 02:48View Solution
02:48View SolutionIf R1 and R2 are the radii of curvature of double convex lens made of same material, the lens with more focal length is
View SolutionCalculate the refractive index of the material of the lens using the given data.

Radius of curvature of the first surface R1=0.2m Radius of curvature of the second surface R2=0.2m.View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as : P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2))) where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R_(1) and R_(2) are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R_(1) and R_(2) with their proper signs as per sign convention being followed by us. Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R_(1)|=|R_(2)|=R" (say)" Let the given biconvex lens be divided in two equal parts, as shown in Fig. (a), along a section YY' which is perpendicular to the principal axis of lens. What is the power of each part?
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is your answer modified if the given biconvex lens is divided into two parts along a section XX' along its principal axis ?View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If twoplanoconvex lenses fromed as a result of (a) are joined together as shown in Fig. (b), what is the net power of the combination ?
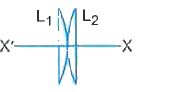 View Solution
View Solution

