निम्नलिखित बिन्दुओ के मध्य दुरी ज्ञात कीजिये।
(t21,2t1) तथा (t22,2t2), जहाँ t1 तथा t2 समीकरण x2−2√3x+2=0 के मूल है।
The correct Answer is:(a) 8,
(b) 2asin∣θ−ϕ2]
Step by step video, text & image solution for निम्नलिखित बिन्दुओ के मध्य दुरी ज्ञात कीजिये। (t_(1)^(2), 2t_(1)) तथा (t_(2)^(2), 2 t_(2)), जहाँ t_(1) तथा t_(2) समीकरण x^(2) - 2 sqrt(3) x + 2 = 0 के मूल है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSAL HINDICHAPTER - सरल रेखा EXERCISE - Exercise - (Special Dpp - 2 )10videos
सरल रेखा
- BOOK - BANSAL HINDICHAPTER - सरल रेखा EXERCISE - Exercise - (Special Dpp - 3 )10videos
सरल रेखा
- BOOK - BANSAL HINDICHAPTER - सरल रेखा EXERCISE - Exercise - (Special Dpp) Special Dpp On Determinant (Integer type /subjective type )6videos
सरल रेखा
- BOOK - BANSAL HINDICHAPTER - सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)EXERCISE - EXERCISE-5 (RANK BOOSTER)13videos
सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)
Similar Questions
बिन्दु R(5, 1) का बिन्दुओ P(2, 10) तथा Q(6, - 2) के सापेक्ष हरात्मक संयुग्मी ज्ञात कीजिये।
12:25View Solution10 इकाई लम्बाई की एक छड़ एक कमरे की एक दीवार तथा फर्श पर स्थित रखी है। यदि छड़ फर्श पर फिसलना प्रारम्भ करती है, तो इसके मध्य बिन्दु का बिन्दुपथ है
02:59View Solutionसारणिक ∣∣ ∣ ∣∣bccaabpqr111∣∣ ∣ ∣∣ का आंकिक मान ज्ञात कीजिये जहाँ a, b, c क्रमशः ह. श्रे. के pth,qth,rth पद है -
03:54View Solutionकिसी चतुष्फलक के शीर्ष A,B,C की स्थिति सदिश क्रमशः (1,1,1),(1,0,0) तथा (3,0,0) है। यदि शीर्ष D से विपरीत तल ABC पर लंब डाला जाता है तथा यह त्रिभुज ABC के शीर्ष A से जाने वाली माध्यिका पर बिंदु E पर मिलता है। यदि AD की लम्बाई 4 तथा चतुष्फलक का आयतन 2√23 है। तो E की स्थिति ज्ञात कीजिए।
05:45View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
02:11View SolutionFind the distances between the following pairs of points (t_(1)^(2),2t_(1)) and (t,@2,2t_(2),),t_(1) and t_(2) are the roots of x^(2)-2sqrt(3)x+2=0
01:07View Solution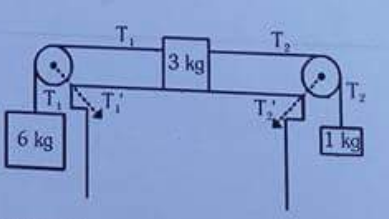
Calculate a, T1,T2,T1'&T2'.View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
05:40View SolutionIf the tangents at t1andt2 to a parabola y2=4ax are perpendicular then (t1+t2)2−(t1−t2)2=
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
06:44View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to03:37View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
04:24View SolutionLet t1=(sin−1x)sin−1x,t2=(sin−1x)cos−1x,t3=(cos−1x)sin−1x,t4=(cos−1x)cos−1x
Match the items of Column I with the items Column II
Column-IColumn-IIA) x∈(0,cos1)p) t1>t2>t4>t3B) x∈(cos1,1√2)q) t4>t3>t1>t2C) x∈(1√2,sin1)r) t1>t2>t4>t3D) x∈(sin1,1)s) t3>t4>t1>t204:05View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
03:24View SolutionThe tangents at the points (at21,2at1),(at22,2at2) are right angles if
View Solution

