Find the average velocity for the time intervals Δt=t2−0.75 when t2 is 1.75,1.5,1.25and 1.0s . What is the instantaneous velocity at t=0.75s?
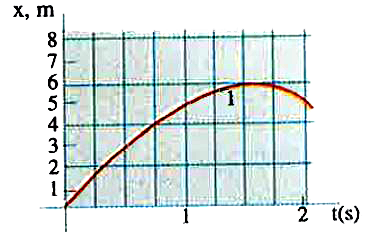
The correct Answer is:About 2ms−1;2.7ms−1;3.2ms−1;4.0ms−1 from slope at 0.75s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE (LEVEL 2)
28 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Questions for Descriptive Answers
7 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Very Short Answer Type Questions
15 Videos
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise
84 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
Similar Questions
Find the average velocity for the time intervals Δt=t2−0.75 when t2 is 1.75 ,1.25 and 1.0 s. What is the instantaneous velocity at t=0.75 s?
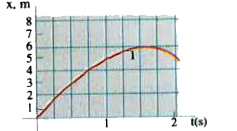
View SolutionThe position of a particle moving along the x axis is given in centimeters by x=9.75+1.50t3, where t is in seconds. Calculate (a) the average velocity during the time interval t=2.00s to t=3.00s, (b) the instantaneous velocity at t=2.00s , (c) the instantaneous velocity at t=3.00s, (d) the instantaneous velocity at t=2.50s, and (e) the instantaneous velocity when the particle is midway between its positions at t=2.00s and t=3.00s . (f) Graph x versus t and indicate your answers graphically
View SolutionA angular positio of a point on the rim of a rotating wheel is given by θ=4t−3t2+t3 where θ is in radiuans and t is in seconds. What are the angualr velocities at
(a).t=2.0 and
(b). t=4.0s
(c). What is the average angular acceleration for the time interval that begins at t=2.0s and ends at t=4.0s?
(d). What are the instantaneous angular acceleration at the biginning and the end of this time interval?
View SolutionA angular positio of a point on the rim of a rotating wheel is given by θ=4t−3t2+t3 where θ is in radiuans and t is in seconds. What are the angualr velocities at
(a).t=2.0 and
(b). t=4.0s
(c). What is the average angular acceleration for the time interval that begins at t=2.0s and ends at t=4.0s?
(d). What are the instantaneous angular acceleration at the biginning and the end of this time interval?
View SolutionThe intantaneous coordinates of a particle are x=(8t−1)m and y=(4t2)m. Calculate (i) the average velocity of the particle during time interval from t=2s to t=4s (ii) the instantaneous velocity of the particle at t=2s.
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View SolutionThe displacement of a particle moving along an x axis is given by x=18t+5.0t2, where x is in meters and t is in seconds. Calculate (a) the instantaneous velocity at t=2.0s and (b) the average velocity between t=2.0s and t=3.0s.
View SolutionThe velocity of a paticle is given by the equation, v=2t2+5cms−1. Find (i) the change in velocity of the velocity of the particle during the time interval between t1=2s and t2=4s (ii) the average acceleration during the same interval and (iii) the instantaneous acceleration at t2=4s.
View SolutionThe angular position of a point on the rim of a rotating wheel is given by θ=4t3−2t2+5t+3 rad. Find
(a) the angular velocity at t=1s,
(b) the angular acceleration at t=2s.
(c ) the average angular velocity in time interval t=0 to t=2s and
(d) the average angular acceleration in time interval t=1 to t=3s.
View Solution
