A long rectangular slab of transparent medium of thickness 'd' placed on a table with its length parallel to the x-axis and width parallel to the y-axis. A ray of light travelling in air makes a near normal incidence on the slab as shown. Taking the point of incidence as origin (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr), where μ1 and r( > d) are constants. The refractive index of air is m0
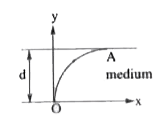
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
r⎧⎨⎩1−√1−(dr)2⎫⎬⎭
r⎧⎨⎩+√1−(dr)2⎫⎬⎭
r⎧⎨⎩1−√1+(dr)2⎫⎬⎭
r⎧⎨⎩1+√1+(dr)2⎫⎬⎭
The correct Answer is:A
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
46 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
98 Videos
Similar Questions
A long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
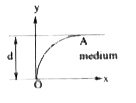
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
View SolutionA light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
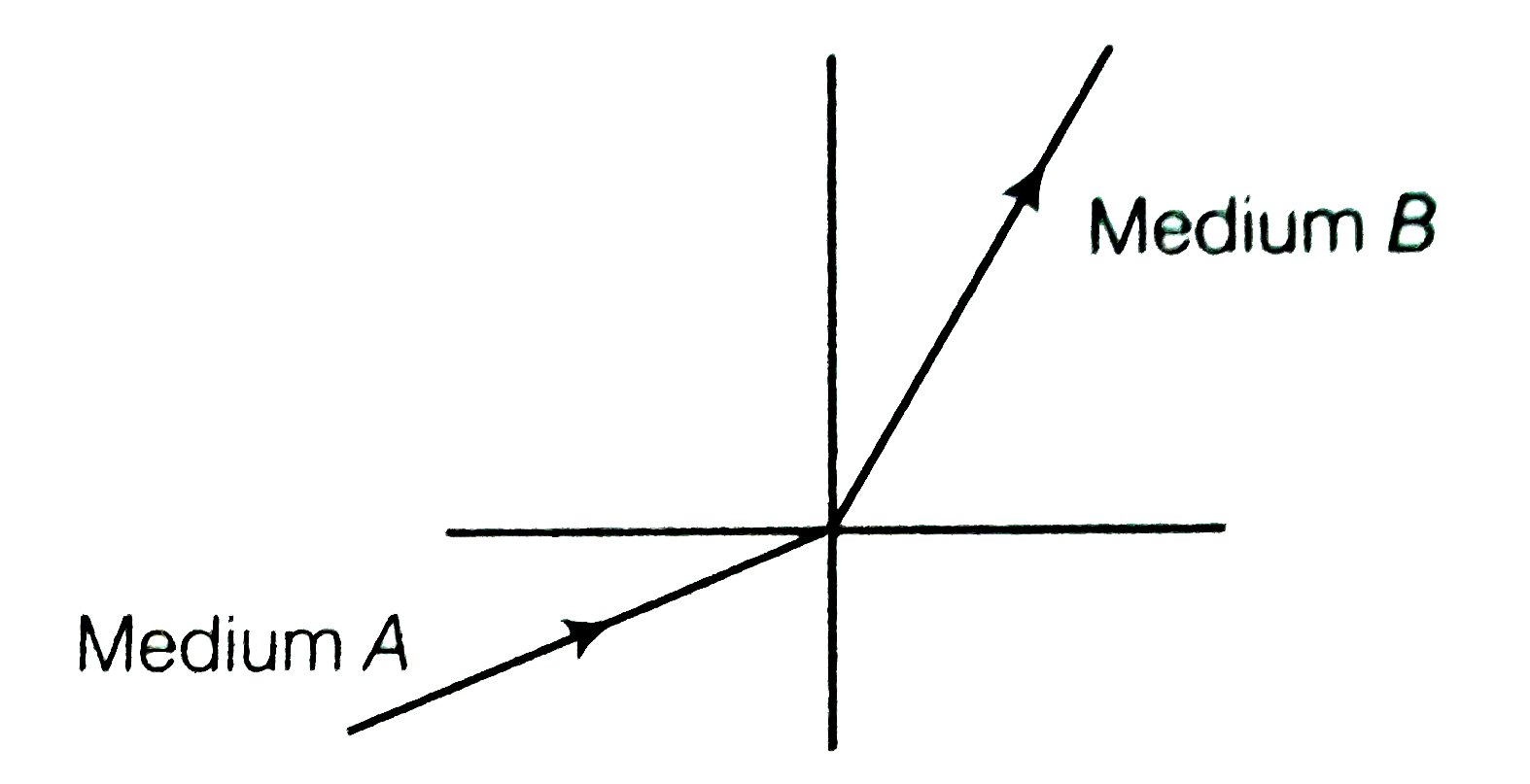
View Solution
Knowledge Check
The ray of light travels from raer medium to denser medium of refractive index μ. The angle of incidence of twice the angle of refraction. The angle of incidence is given by
A2sin−1(μ2)B2cos−1(2μ)C2cos−1(μ2)Dsin−1(μ2)
A ray of light travelling in air is incident at grazing angle (incident angle = 90∘) on a large rectangular slab of a transparent medium of thickness t = 1 m. The point of incidence js the origin A (0, 0). The medium has a refractive index of n (y) given
n(y)=(9ky32+1)12
Where K = (meter)−32, The refractive index of air is 1.
Obtain the equation for the trajectory y(x) of the ray of the medium.
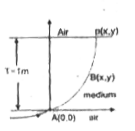
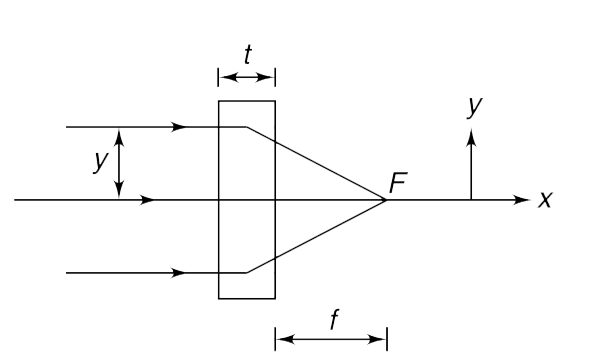
View SolutionA parallel beam of light travelling in x direction is incident on a glass slab of thickness t. The refractive index of the slab changes with y as μ=μ0(1–y2y02)where μ0 is the refractive index along x axis and y0 is a constant. The light beam gets focused at a point F on the x axis. By using the concept of optical path length calculate the focal length f. Assumef>>t and consider y to be small.
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
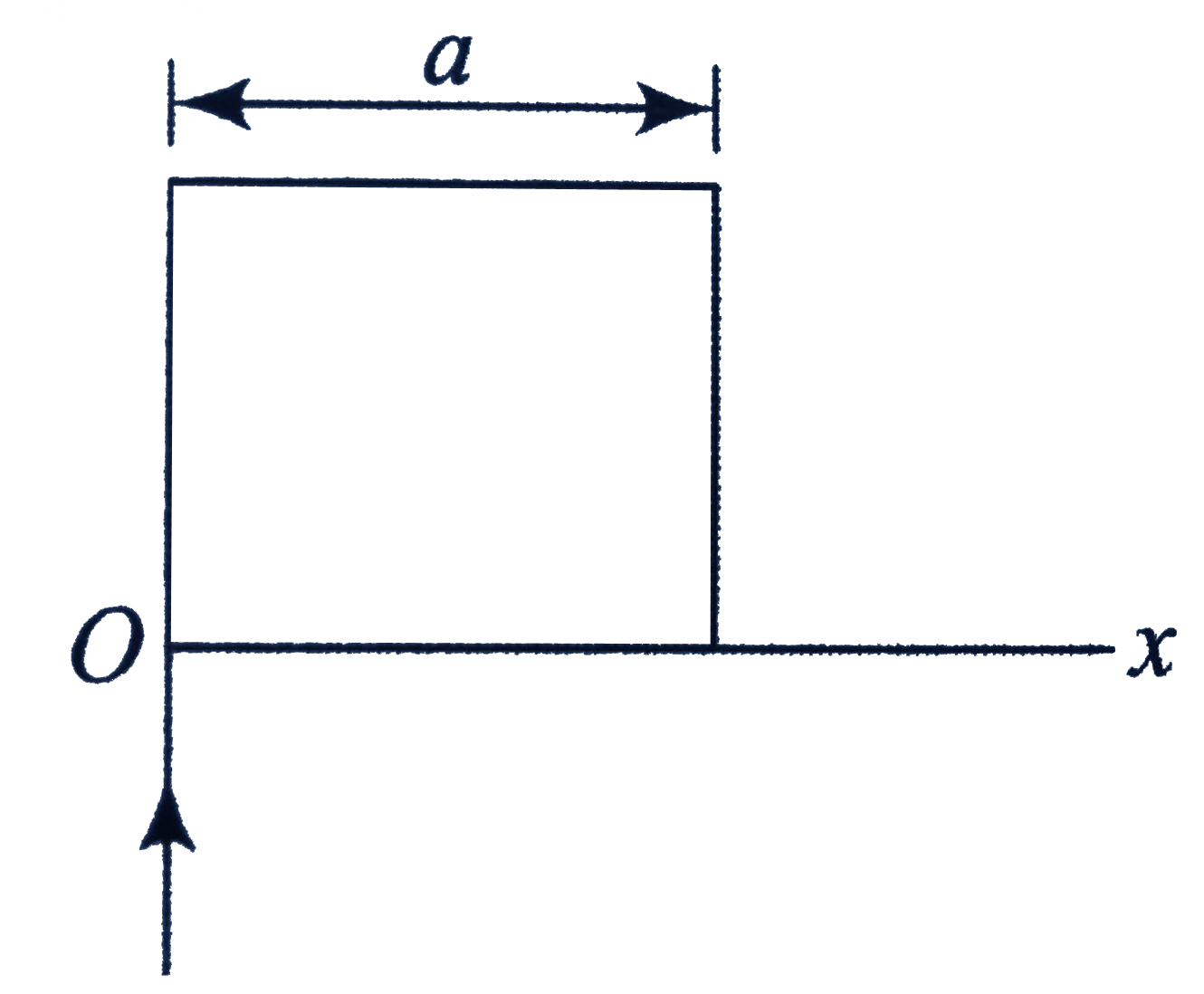
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .

View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light travelling in a medium of refractive index μ1 is incident obliquely at the boundary of a medium of refractive index μ2. The ray may reflect back totally only when u1 is _____ μ2.
View Solution
