A long rectangular slab of transparent medium of thickness 'd' placed on a table with its length parallel to the x-axis and width parallel to the y-axis. A ray of light travelling in air makes a near normal incidence on the slab as shown. Taking the point of incidence as origin (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr), where μ1 and r( > d) are constants. The refractive index of air is m0
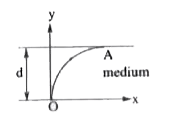
The refractive index μA of the medium at A
μ0√1−(dr)2
μ0√1−(dr)2
−μ0√1+(rd)2
μ0√1+(dr)2
The correct Answer is:B
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
46 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
98 Videos
Similar Questions
A long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
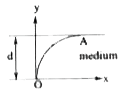
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View Solution
Knowledge Check
The ray of light travels from raer medium to denser medium of refractive index μ. The angle of incidence of twice the angle of refraction. The angle of incidence is given by
A2sin−1(μ2)B2cos−1(2μ)C2cos−1(μ2)Dsin−1(μ2)A ray of light, travelling in a medium of refractive index mu, is incident at an angle i on a composite transparent plate consisting of three plates of refractive indices μ1,μ2andμ3. The ray emerges from the composite plate into a medium of refractive index μ4, at angle x. Then,
Asinx=siniBsinx=μμ4siniCsinx=μ4μsiniDsinx=μ1μ3μμ2μ2μ4sini
The refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .

View SolutionA light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
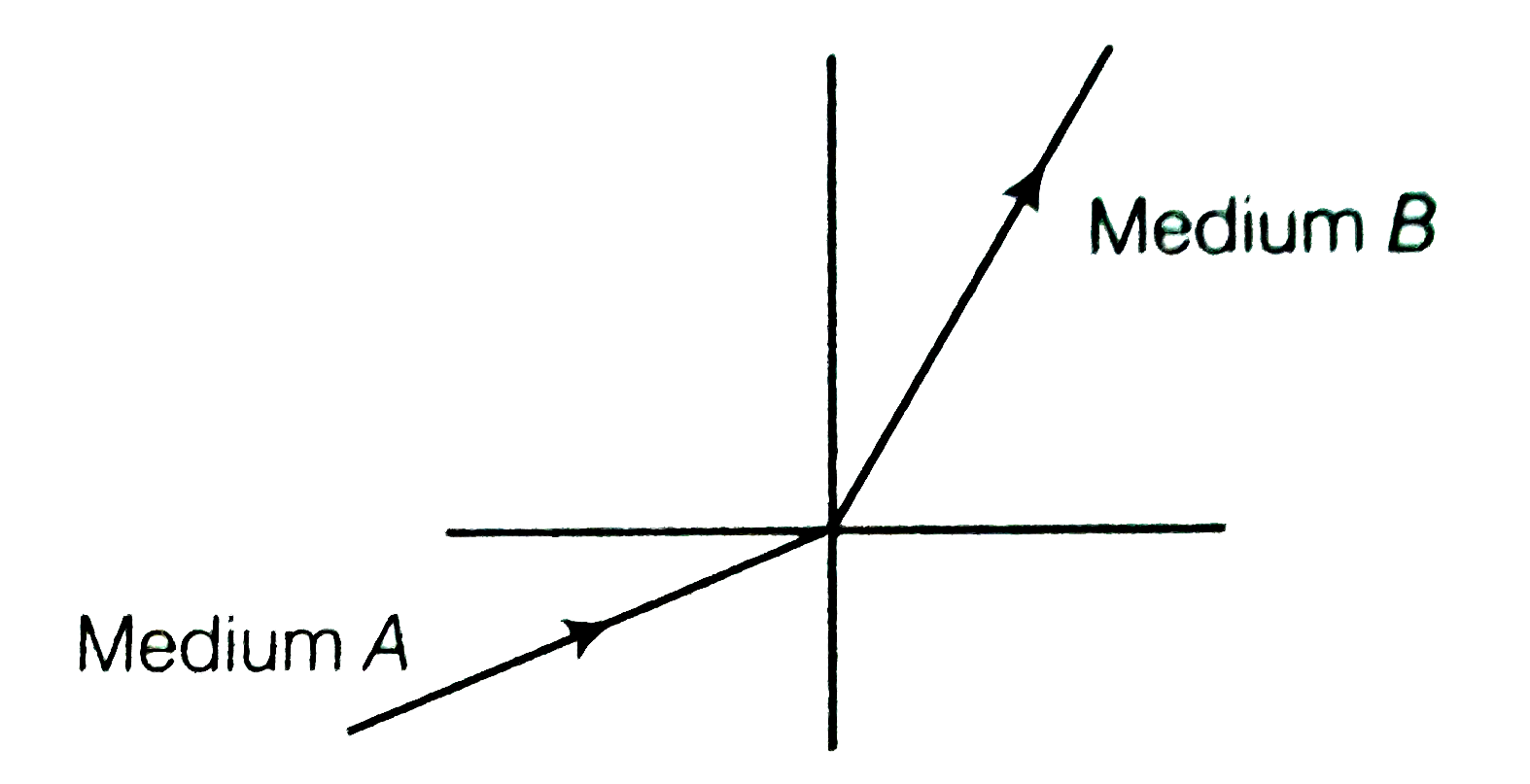
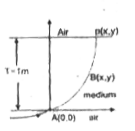
View SolutionA ray of light travelling in air is incident at grazing angle (incident angle = 90∘) on a large rectangular slab of a transparent medium of thickness t = 1 m. The point of incidence js the origin A (0, 0). The medium has a refractive index of n (y) given
n(y)=(9ky32+1)12
Where K = (meter)−32, The refractive index of air is 1.
Obtain the equation for the trajectory y(x) of the ray of the medium.
View SolutionA parallel incident beam falls on a solid glass sphere at near normal incidence.Show that the image in terms of the index of refractive μ and the sphere of radius R is given by
R(2−μ)2(μ−1)
View SolutionA parallel incident beam falls on a solid glass sphere at near normal incidence.Show that the image in terms of the index of refractive μ and the sphere of radius R is given by
R(2−μ)2(μ−1)
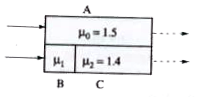
View SolutionA slab of transparent materials is made as shown in the figure. Monochromatic parallel beams of light are normally incident on the slabs. The thickness of C is twice the thickness of B. The number of waves is A= the number of waves in the combination of B and C. The refractive index of material A is μ0=1.5 and that of C is μ2=1.4
View Solution
