If on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If or does not exist and the second derivative changes sign when passing through the point then the point is the = point of inflection of the curve y=f(x)
is concave along the entire number scale thenSolution in Telugu
The correct Answer is:C
Step by step video, text & image solution for If f^(11)(x)lt0(gt0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f^(11)(x_(0))=0 or does not exist and the second derivative changes sign when passing through the point x_(0) then the point (x_(0),f(x)) is the = point of inflection of the curve y=f(x) y=x^(4)+ax^(3)+(3)/(2)x^(2)+1 is concave along the entire number scale then by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II)(INTEGER TYPE QUESTIONS)4videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN)) (STRAIGHT OBJECTIVE TYPE QUESTIONS)50videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II) (MATRIX MATCHING TYPE QUESTIONS)2videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III35videos
MAXIMA & MINIMA
- BOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )2videos
MEAN VALUE THEOREMS
Similar Questions
A right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______
02:58View SolutionThe minimum value of (A2+A+1)(B2+B+1)(C2+C+1)(D2+D+1)BACD , wher A,B,C,D are positive
01:42View SolutionLet f(x) be a real valued function defined by f(x)=x2−2|x| an
g(x) 02:49View Solution
02:49View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
05:08View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )View Solutionif |f(x_(1))-f(x_(2))|<=(x_(1)-x_(2))^(2) Find the equation of gent to the curve y=f(x) at the point (1,2).
05:01View SolutionThe derivative of f(x)=3|2+x| at the point x_(0)=-3 is
03:16View SolutionThe area bounded by the curve y=f(x) (where f(x)>=0) ,the co-ordinate axes & the line x=x_(1) is given by x_(1).e^(x_(1)). Therefore f(x) equals
07:56View SolutionIf y=f(x) is a curve and if there exists two points A(x_(1),f(x_(1))) and B(x_(2),f(x_(2))) on it such that f'(x_(1))=-(1)/(f(x_(2))), then the tangent at x_(1) is normal at x_(2) for that curve. Now,answer the following questions.
04:49View SolutionThe graph of the derivative f of a continuous function f is shown with f(0)=0

If f(x) has local minima at x=x1 and x=x2,f has inflection point at x=k, number of critical points of y=f(x) is w then x1+x2−k−w is...........07:17View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
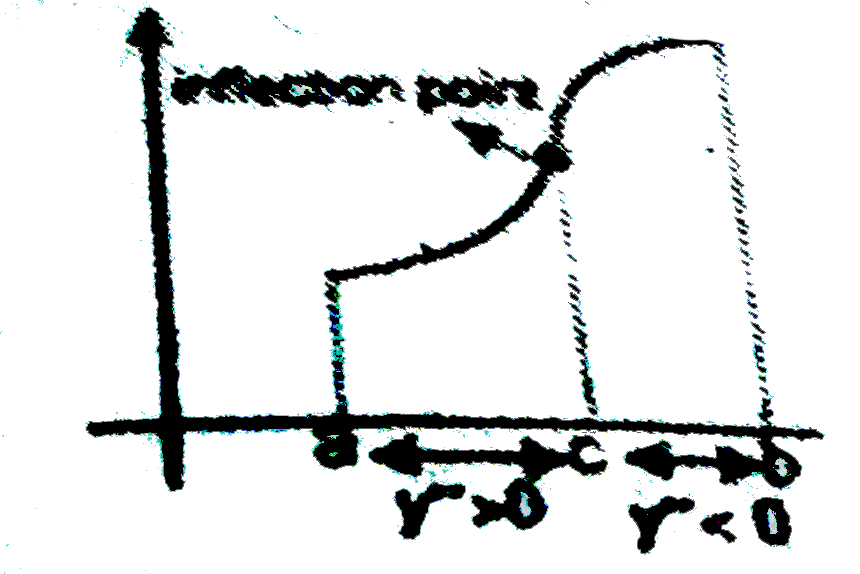
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :04:29View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
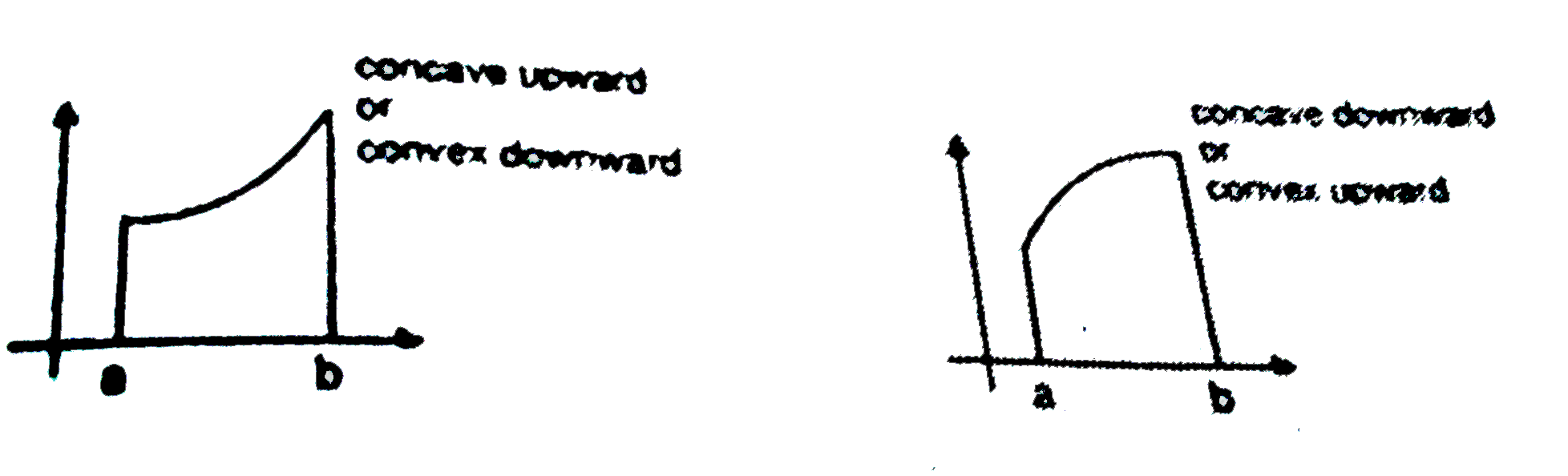
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :07:12View SolutionIf y=f(x) is a curve and if there exists two points A(x1,f(x1)andB(x2,f(x2) on it such that f'(x1)=−1f'(x2)=f(x2)−f(x1)x2−x1, then the tangent at x1 is normal at x2 for that curve. Now, anwer the following questions.
Number of such lines on the curve y2=x3, is06:32View SolutionDetermine the intervals of concavity of the curve f(x)=(x−2)3(x−4),x∈R and the points of inflection if any.
06:32View SolutionDetermine the intervals of concavity of the curve f(x)=(x−1)3(x−5),x∈R and , points of inflection if any
04:36View Solution

