If f11(x)<0(>0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f11(x0)=0 or does not exist and the second derivative changes sign when passing through the point x0 then the point (x0,f(x)) is the = point of inflection of the curve y=f(x)
If y=x4+x3−18x2+24x−12 thenSolution in Telugu
y has only teo points of inflection
y has only 4 points of inflection
π4 is the only point of inflection
y has infinite number of points of inflection
The correct Answer is:D
Step by step video, text & image solution for If f^(11)(x)lt0(gt0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f^(11)(x_(0))=0 or does not exist and the second derivative changes sign when passing through the point x_(0) then the point (x_(0),f(x)) is the = point of inflection of the curve y=f(x) If y=x^(4)+x^(3)-18x^(2)+24x-12 then by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II)(INTEGER TYPE QUESTIONS)4videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN)) (STRAIGHT OBJECTIVE TYPE QUESTIONS)50videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II) (MATRIX MATCHING TYPE QUESTIONS)2videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III35videos
MAXIMA & MINIMA
- BOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )2videos
MEAN VALUE THEOREMS
Similar Questions
A right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______
01:42View SolutionThe minimum value of (A2+A+1)(B2+B+1)(C2+C+1)(D2+D+1)BACD , wher A,B,C,D are positive
04:51View SolutionLet f(x) be a real valued function defined by f(x)=x2−2|x| an
g(x) 01:15View Solution
01:15View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )05:01View SolutionThe derivative of f(x)=3|2+x| at the point x_(0)=-3 is
03:16View Solutionf(x)=x3at x=0 has inflection point y''=0 at x=0 and change sign.
07:56View SolutionA critical point x_(0) of the function f(x)=x^(3) is selected at random.The probability that f is extremum at x_(0) is
04:49View SolutionThe graph of the derivative f of a continuous function f is shown with f(0)=0

If f(x) has local minima at x=x1 and x=x2,f has inflection point at x=k, number of critical points of y=f(x) is w then x1+x2−k−w is...........04:29View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
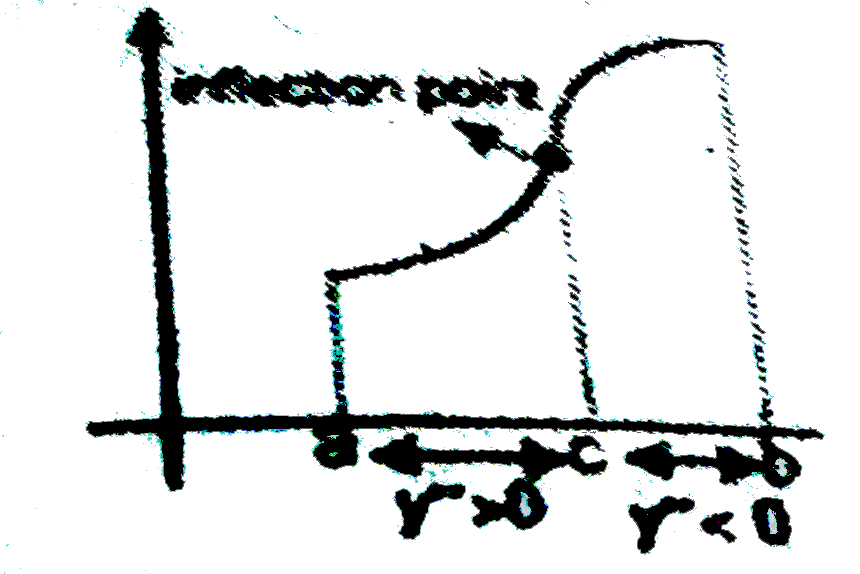
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :07:12View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
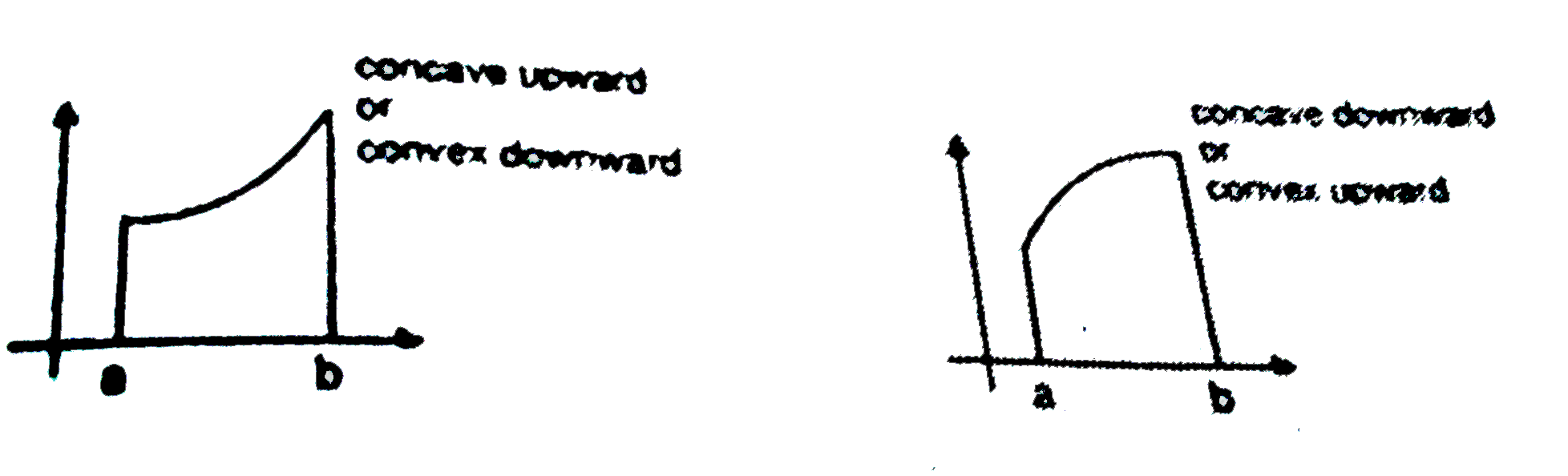
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :06:32View SolutionIf y=f(x) is a curve and if there exists two points A(x1,f(x1)andB(x2,f(x2) on it such that f'(x1)=−1f'(x2)=f(x2)−f(x1)x2−x1, then the tangent at x1 is normal at x2 for that curve. Now, anwer the following questions.
Number of such lines on the curve y2=x3, is03:21View SolutionDetermine the intervals of concavity of the curve f(x)=(x−2)3(x−4),x∈R and the points of inflection if any.
04:36View SolutionIf x0 is the x - coordinate of the point of inflection of a curve y=f(x) then (second derivative exists) ………….. .
View Solutionसभी x1,x2∈R के लिए यदि |f(x1)−f(x2)|<(x1−x2)2 है। बिंदु (1,2) पर वक्र y=f(x) की स्पर्श रेखा की समीकरण ज्ञात कीजिए।
04:22View Solution

