At the initial moment three points A, B and C are on a horizontal straight line at equal distances from one another. Point A begins to move vertically upward with a constant velocity v and point C vertically downward without any initial velocity but with a constant acceleration a. How should point B move vertically for all the three points to be constantly on one straight line. The points begin to move simultaneously.
The correct Answer is:A, B, C, D
To solve the problem, we need to determine how point B should move vertically so that points A, B, and C remain in a straight line at all times. Let's break down the solution step by step.
Step 1: Understand the Initial Setup
We have three points A, B, and C on a horizontal line, equally spaced. Let's denote the distance between each point as d. At time t=0:
- Point A is at position A(0,0) and moves upward with a constant velocity v.
- Point B is at position B(0,d) and will move vertically (we need to determine how).
- Point C is at position C(0,2d) and moves downward with an initial velocity of 0 and a constant acceleration a.
Step 2: Write the Equations of Motion
For point A moving upward:
- The position of A at time t is given by:
yA=vt
For point C moving downward:
- The position of C at time t is given by:
yC=2d−12at2
(Note: The downward motion is considered negative.)
Let the position of point B at time t be:
yB=yB(t)
We need to find the function yB(t) such that points A, B, and C remain collinear.
Step 3: Condition for Collinearity
For points A, B, and C to be collinear, the slopes between these points must be equal. This can be expressed as:
yA−yB0−0=yB−yC0−0
This condition simplifies to:
(yA−yB)=k(yB−yC)
where k is a proportionality constant that remains the same for the slopes.
Step 4: Substitute the Positions
Substituting the equations of motion into the collinearity condition:
(vt−yB)=k(yB−(2d−12at2))
Step 5: Solve for yB
Rearranging gives:
vt−yB=k(yB−2d+12at2)
This can be solved for yB to find how point B must move.
Step 6: Equate and Simplify
By isolating yB and simplifying, we can find the relationship between v, a, and the motion of point B. After some algebra, we find:
yB=v2t−a2t2+(constant)
Step 7: Final Result
The final expression indicates that point B must move with an initial velocity of v2 and an acceleration of −a2 in the vertical direction.
Summary
To keep points A, B, and C in a straight line:
- Point B should move vertically with an initial velocity of v2 and an acceleration of −a2.
We have three points A, B, and C on a horizontal line, equally spaced. Let's denote the distance between each point as d. At time t=0:
- Point A is at position A(0,0) and moves upward with a constant velocity v.
- Point B is at position B(0,d) and will move vertically (we need to determine how).
- Point C is at position C(0,2d) and moves downward with an initial velocity of 0 and a constant acceleration a.
For point A moving upward:
- The position of A at time t is given by:
yA=vt
- The position of C at time t is given by:
yC=2d−12at2
(Note: The downward motion is considered negative.)
yB=yB(t)
We need to find the function yB(t) such that points A, B, and C remain collinear.
For points A, B, and C to be collinear, the slopes between these points must be equal. This can be expressed as:
yA−yB0−0=yB−yC0−0
This condition simplifies to:
(yA−yB)=k(yB−yC)
where k is a proportionality constant that remains the same for the slopes.
Substituting the equations of motion into the collinearity condition:
(vt−yB)=k(yB−(2d−12at2))
Rearranging gives:
vt−yB=k(yB−2d+12at2)
This can be solved for yB to find how point B must move.
By isolating yB and simplifying, we can find the relationship between v, a, and the motion of point B. After some algebra, we find:
yB=v2t−a2t2+(constant)
The final expression indicates that point B must move with an initial velocity of v2 and an acceleration of −a2 in the vertical direction.
To keep points A, B, and C in a straight line:
- Point B should move vertically with an initial velocity of v2 and an acceleration of −a2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE39videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE23videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
Knowledge Check
- Question 1 - Select One
A player throws a ball vertically upwards with velocity u. At highest point,
A1. both the velocity and acceleration of the ball are zero.B2. the velocity of the ball is u but its accelerationC3. the velocity of the ball is zero but its acceleration is g.D4. the velocity of the ball is u but its acceleration is g. - Question 2 - Select One
Two stones are thrown from the same point with velocity of 5 ms−1 one vertically upwards and the other vertically downwards. When the first stone is at the highest point the relative velocity of the second stone with respect to the first stone is,
A5ms−1B0ms−1C10ms−1D−5ms−1
Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionA particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
View SolutionA ball is thrown vertically upwards with an initial velocity of 5m/sec from point P as shown Q is a point 10m vertically below the point P. Then the speed of ball at point Q will be : (take g=10m/s2 and neglect air resistance)
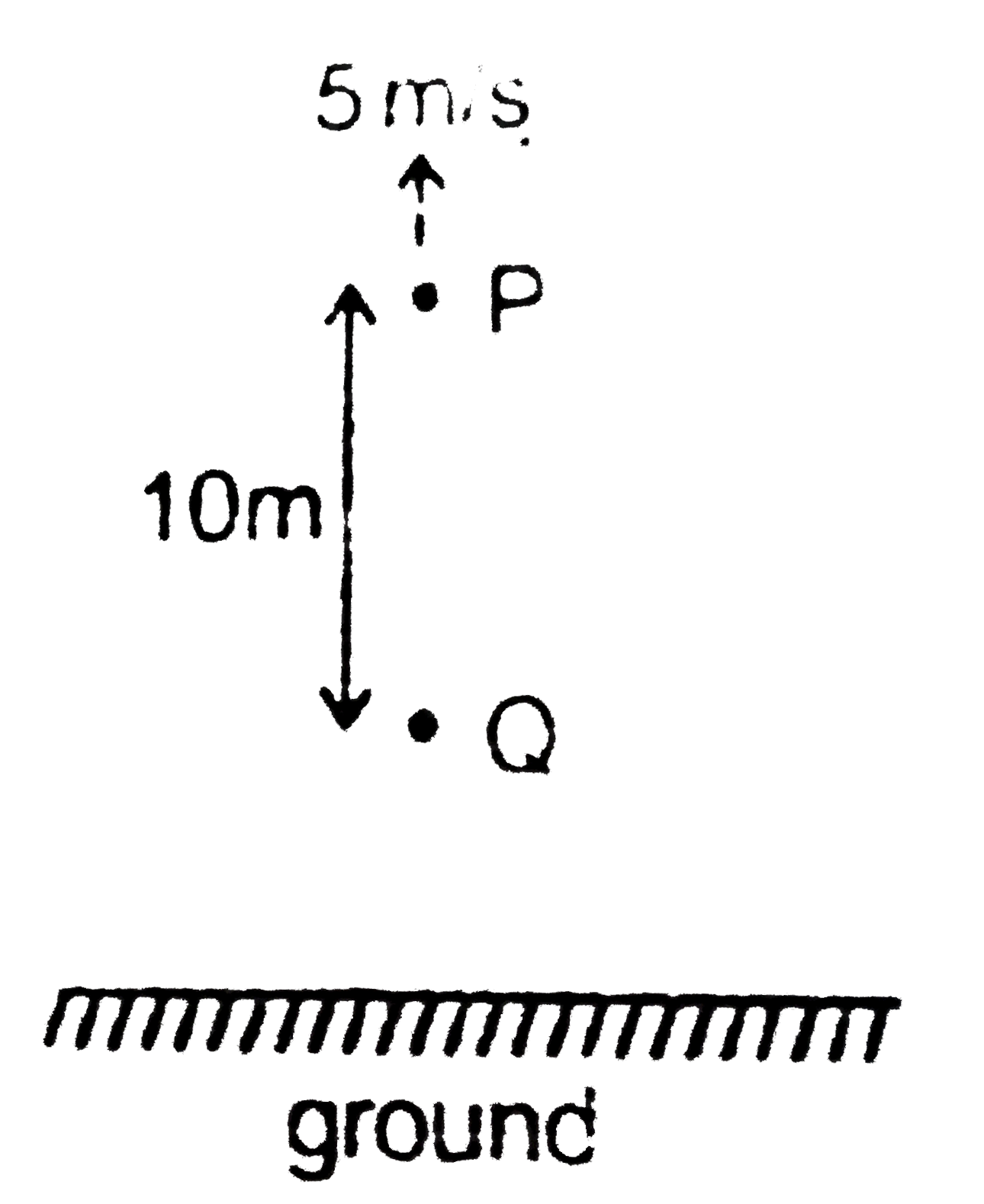 View Solution
View SolutionA stone is dropped freely while another thrown vertically downward with an initial velocity of 4 m/s from the same point simultaneously. The distance of separation between them will become 30 m after a time of
View SolutionFind the period of oscillation of a pendulum of length l if its point of suspension is
(a) moving vertically up with acceleration a
(b) moving vertically down with acceleration a(<g)
(c) failing freely under gravity
moving horizontal with acceleration a.View SolutionA particle P is projected with velocity u1 at an angle of 30∘ with the horizontal. Another particle Q is thrown vertically upwards with velocity u2 from a point vertically below the highest point of path of P. Determine the necessary condition for the two particles to collide at the highest point.
 .View Solution
.View Solution

