The slopes of wind screen of two cars are α1=30∘andα2=15∘ respectively. At what ratio v1v2 of the velocities of the cars will their drivers see the hail stones bounced back by the wind screen on their cars in vertical direction? Assume hail stones fall vertically downwards and collisions to be elastic.
The correct Answer is:A, B, C
To solve the problem, we need to determine the ratio of the velocities v1/v2 of two cars such that the drivers see hailstones bouncing back from their windscreens in a vertical direction. The slopes of the windscreens are given as α1=30∘ and α2=15∘.
1. Understanding the Problem:
- Hailstones fall vertically downwards with a velocity v.
- The cars are moving with velocities v1 and v2.
- The angle of incidence β1 for the hailstone on the first car's windscreen and β2 for the second car's windscreen can be related to the slopes α1 and α2.
2. Setting Up the Geometry:
- For the first car, the slope of the windscreen is α1, and for the second car, it is α2.
- The angle of incidence β1 can be expressed as:
β1=90∘−α1=90∘−30∘=60∘
- Similarly, for the second car:
β2=90∘−α2=90∘−15∘=75∘
3. Using the Law of Reflection:
- For the hailstones to bounce back vertically, the angle of incidence must equal the angle of reflection. Therefore, we have:
α1+2β1=90∘andα2+2β2=90∘
4. Relating Velocities:
- The relationship between the velocities and angles can be derived from the tangent function:
tan(α)=vvi
- For the first car:
tan(α1)=vv1
- For the second car:
tan(α2)=vv2
5. Finding the Ratio of Velocities:
- We can express the ratio of the velocities as:
v1v2=tan(α2)tan(α1)
- Substituting the angles:
v1v2=tan(15∘)tan(30∘)
6. Calculating the Tangents:
- We know:
tan(30∘)=1√3andtan(15∘)=2−√3
- Thus:
v1v2=2−√31√3=(2−√3)⋅√3=2√3−3
7. Final Result:
- The ratio of the velocities v1/v2 is approximately 3:1.
- Hailstones fall vertically downwards with a velocity v.
- The cars are moving with velocities v1 and v2.
- The angle of incidence β1 for the hailstone on the first car's windscreen and β2 for the second car's windscreen can be related to the slopes α1 and α2.
- For the first car, the slope of the windscreen is α1, and for the second car, it is α2.
- The angle of incidence β1 can be expressed as:
β1=90∘−α1=90∘−30∘=60∘
- Similarly, for the second car:
β2=90∘−α2=90∘−15∘=75∘
- For the hailstones to bounce back vertically, the angle of incidence must equal the angle of reflection. Therefore, we have:
α1+2β1=90∘andα2+2β2=90∘
- The relationship between the velocities and angles can be derived from the tangent function:
tan(α)=vvi
- For the first car:
tan(α1)=vv1
- For the second car:
tan(α2)=vv2
- We can express the ratio of the velocities as:
v1v2=tan(α2)tan(α1)
- Substituting the angles:
v1v2=tan(15∘)tan(30∘)
- We know:
tan(30∘)=1√3andtan(15∘)=2−√3
- Thus:
v1v2=2−√31√3=(2−√3)⋅√3=2√3−3
- The ratio of the velocities v1/v2 is approximately 3:1.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE39videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE23videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
The front wind screen of a car is inclined at an 60∘ with the vertical. Hailstones fall vertically downwards with a speed of 5√3ms−1. Find the speed of the car so that hailstones are bounced back by the screen in vertically upward direction with respect to car. Assume elastic collision of hailstones with wind screen.
View SolutionA bird flies to and fro between two cars wich move with velocities v1 and v2, If the speed of the bird is v3 and the initial distance ofseparation between then is d, find the total distance covered bythe bird till the cars meet.
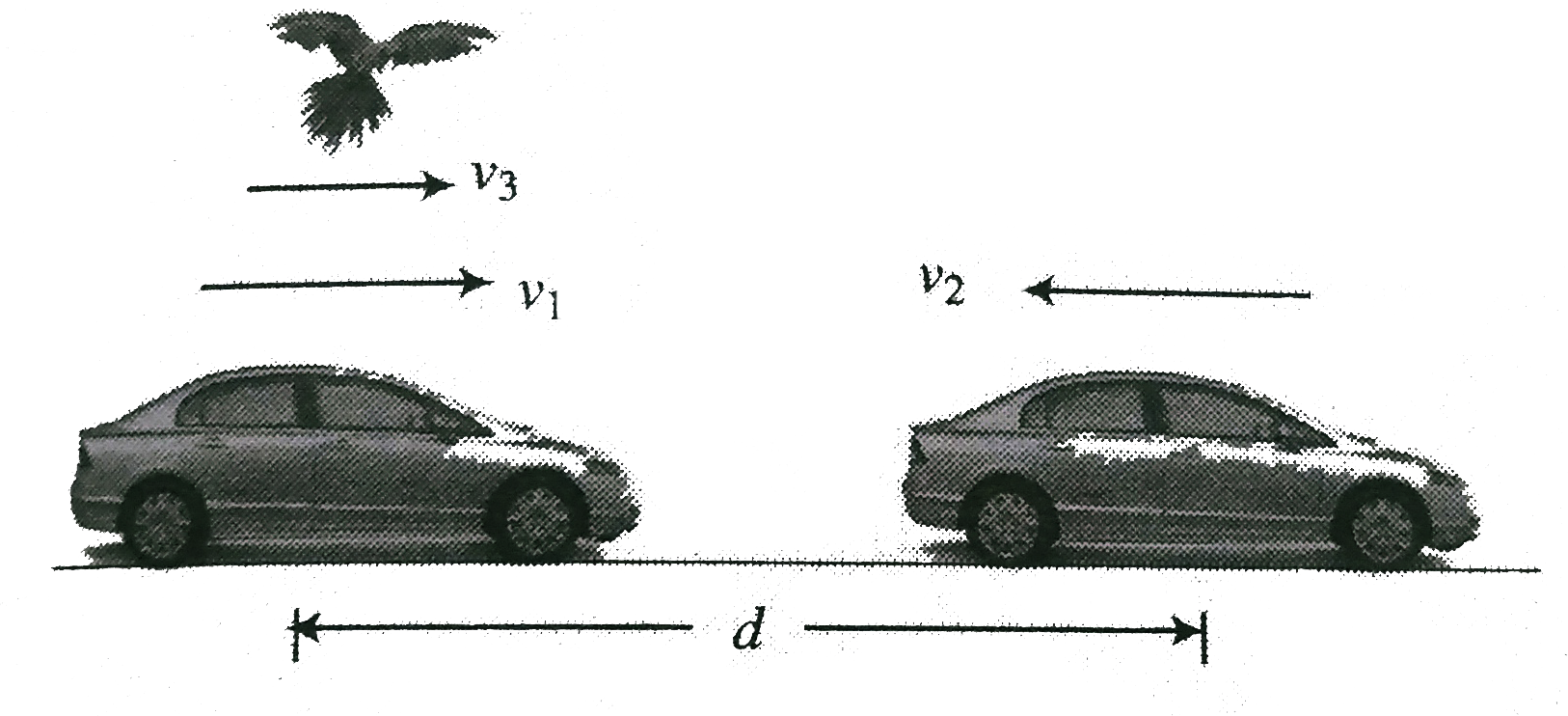 . View Solution
. View SolutionA glass wind screen whose inclination with the vertical can be changed is mounted on a car. The moves horizontally with a speed of 2m/s. At what angle α with the vertical should the wind screen placed so that the rain drops falling vertically downwards with velcoity 6m/s strike the wind screen perpendicularly?
View SolutionTwo racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.

The magnitude of relative acceleration of two cars when car 'A' just reaches the end of circular arc of radius Y.View SolutionHailstones falling vertically with a speed of 10ms−1, hit the wind screen (wind screen makes an angle 30∘ with the horizontal) of a moving car and rebound elastically. Find the velocity of the car if the driver finds the hailstones rebound vertically after striking.
 .View Solution
.View SolutionTwo hail stones with radii in the ratio of 1:2 fall from a great height through the atmosphere. Then the ratio of their momentum after they have attained terminal velocity is
View SolutionTwo cars A and B are moving in same direction with velocities 30 m/s and 20 m/s. When car A is at a distance d behind the car B, the driver of the car A applies brakes producing uniform retardation of 2m/s2. There will be no collision when :-
View SolutionTwo racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.

Which of the following statements is incorrect.View SolutionTwo racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
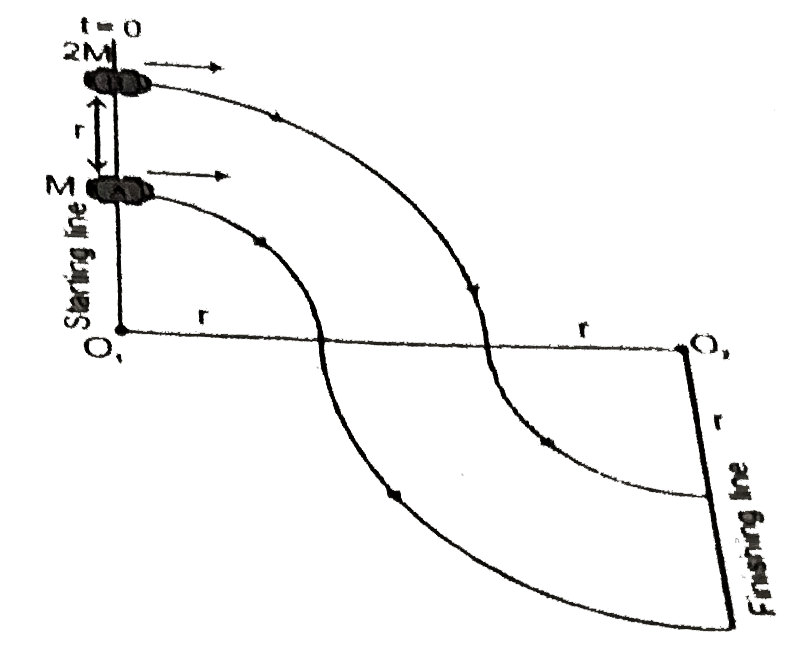
Graph between the magnitude of relative velocity of the two car and time is :View SolutionTwo racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
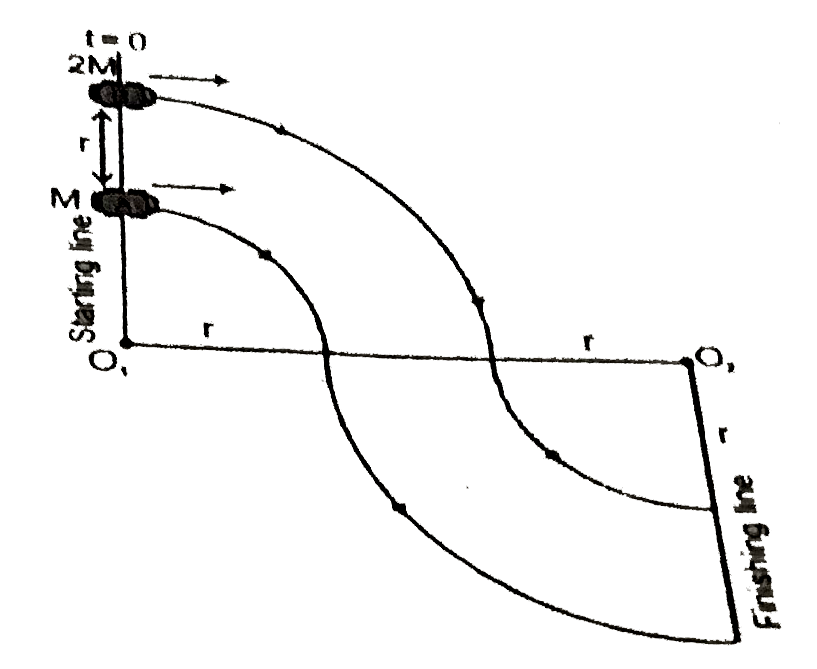
The time interval during which the two cars have same angular speed :View Solution

