In the abjoining figure, wire PQ is smooth, ring A has a mass 1kg and block B,2kg. If system is released from rest with θ=60∘,find
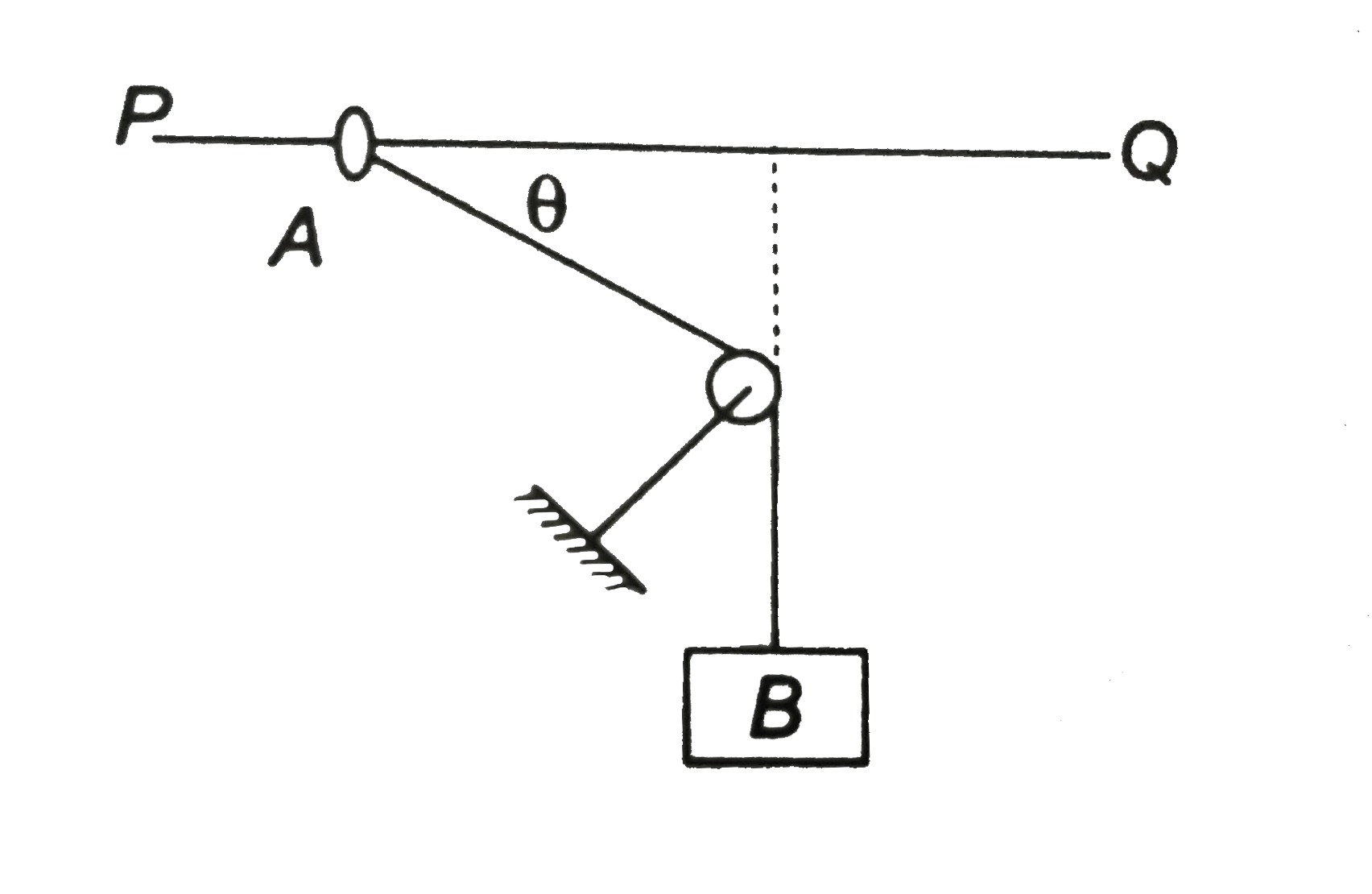
(a)constraint relation between their velocities as a function of θ.
(b) constrain relation between their accelerations just after the release at θ=60∘.
(c) tension in the string and the value of these accelerations at this instant.
M and Q are two fixed fixed points. Therefore.
MQ=contant=c
l=length of string=contant
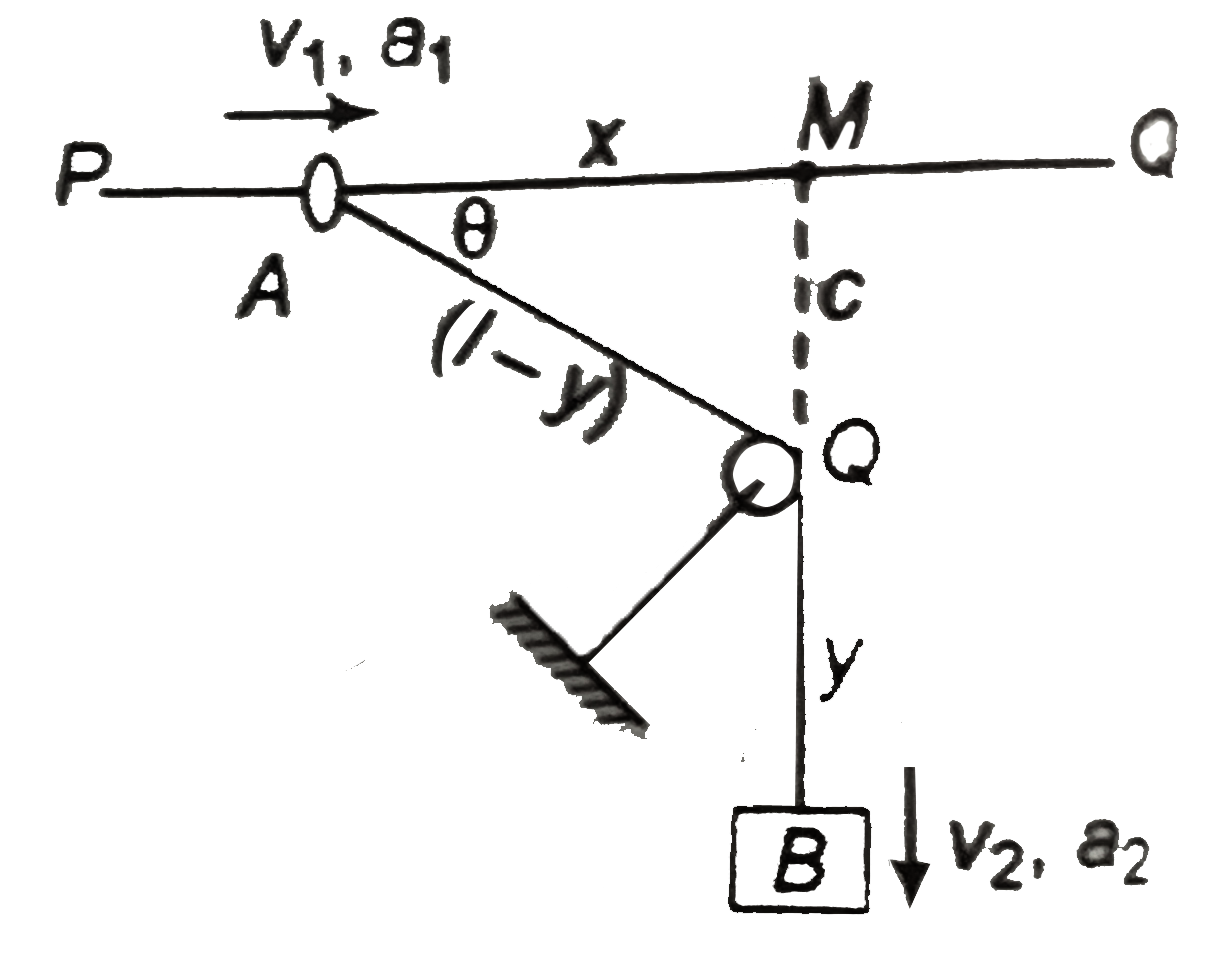 (a) In traingle MQA,(l−y)2=x2+c2
(a) In traingle MQA,(l−y)2=x2+c2
Differentiating w.r.t time, we get
2(l−y)(−dydt)=2x(+dxdt)+0
or (l−y)(+dydt)=x(−dxdt) ...(i)
∴dydt=(xl−y)(−dxdt) ...(ii)
y is increasing with time,
∴+dydt=u2
x is increasing with time,
∴−dxdt=u1 and xl−y=cosθ
Substituting these value in Eq (ii) we have
u2=u1cosθ
(b) Further differentiating Eq. (i) we have,
d2ydt2(l−y)−(dydt)2=−[xd2xdt2+(dxdt)2] ...(iii)
Just after the release, u1,u2,dxdt and dydt all are zero.Substituting in Eq. (iii), we have ,
d2ydt2=(xl−y)(d2xdt2) ...(iv)
Here d2ydt2=a2and−d2xdt2=a1
xl−y=cos60∘=12
Substituting in Eq. (iv), we have a2=a12 ...(v)
(c) For A Equation is

T=cos60∘=mAa1
or T2=(1)a1=a1 ...(vi)
For B 20−T=mBa2
20−T=2a2 ...(vii)
Solving Eqs.(v),(vi) and (vii), we get
T=403N⇒a1=203m/s2
a2=103m/s2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples9videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.110videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
Consider the system shown in fig. the system is released from rest, find the tension in the cord connected between 1kg and 2 kg blocks.
 View Solution
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
 View Solution
View SolutionConsider the system shown in fig. the system os released from rest, find the tension in the cord connected between 1kg and 2 kg blocks.
 View Solution
View SolutionThe pulley is light and smooth: the strings are inextensible and light. The system is released from rest, find the acceleration of each block, tensions in the strings and reaction in pulley.
 View Solution
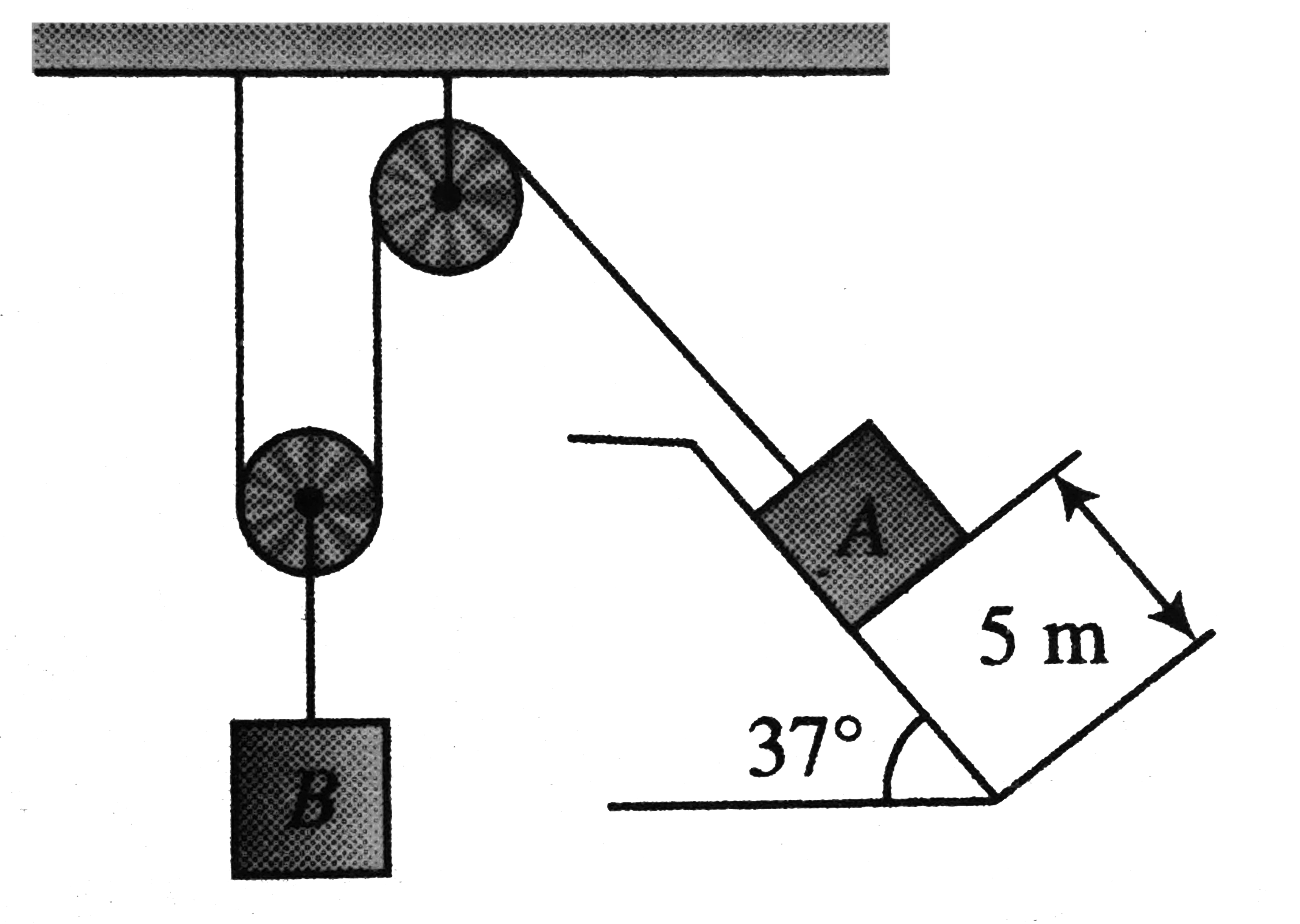
View SolutionThe blocks A and B shown in figure have masses MA=5kg and MB=4kg. The system is released from rest. The speed of B after A has travelled a distance 1m along the incline is
 View Solution
View SolutionA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is
 View Solution
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
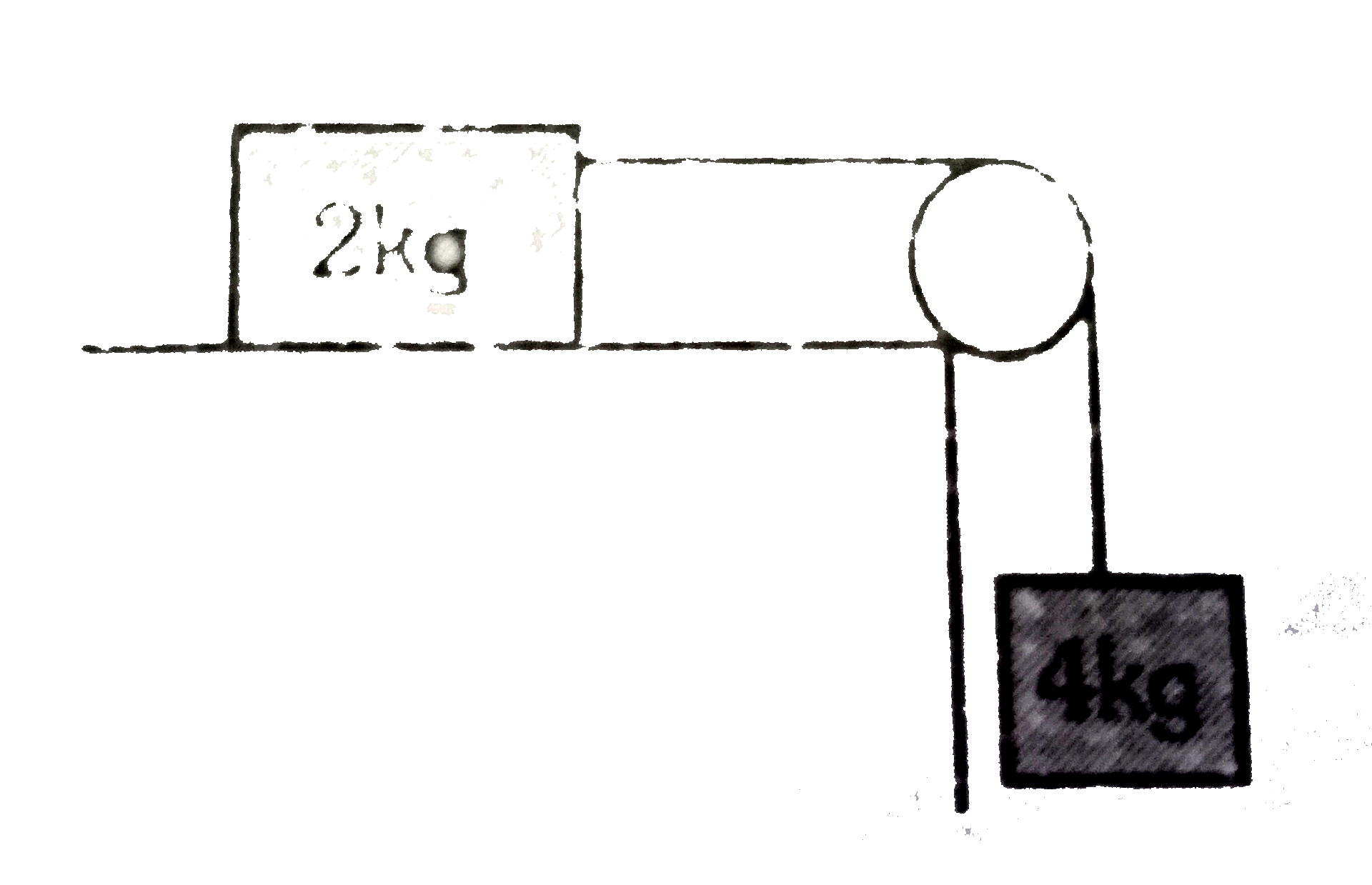 View Solution
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
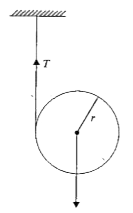 View Solution
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.

a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View Solution

