On a horizontal rough road , value of coefficient of friction μ=0.4.Find the minimum time in which a distance of 400m can be covered. The car start from rest and finally comes to rest.
To solve the problem, we need to determine the minimum time required for a car to cover a distance of 400 meters on a rough horizontal road, given that the coefficient of friction (μ) is 0.4. The car starts from rest and eventually comes to rest.
1. Identify the Given Data:
- Coefficient of friction, μ = 0.4
- Distance to be covered, S = 400 m
- Initial velocity, u = 0 m/s (the car starts from rest)
- Final velocity, v = 0 m/s (the car comes to rest)
2. Calculate Maximum Acceleration:
The maximum acceleration (a) of the car can be calculated using the formula:
a=μ⋅g
where g is the acceleration due to gravity (approximately 10m/s2).
a=0.4⋅10=4m/s2
3. Determine the Time of Acceleration and Deceleration:
Since the car accelerates to a certain speed and then decelerates back to rest, we can denote the time taken to accelerate as t and the time taken to decelerate as t as well (the times are equal for minimum time).
The distance covered during acceleration (S1) and deceleration (S2) can be expressed using the equation of motion:
S=ut+12at2
Since the initial velocity u=0:
S1=12at2(for acceleration)
S2=12at2(for deceleration)
The total distance covered is:
S=S1+S2=12at2+12at2=at2
Setting this equal to the total distance of 400 m:
at2=400
Substituting a=4m/s2:
4t2=400
t2=4004=100
t=10s
4. Calculate Total Time:
Since the total time includes both the acceleration and deceleration phases:
Total time=t+t=10+10=20s
Final Answer:
The minimum time in which the car can cover a distance of 400 m is 20 seconds.
- Coefficient of friction, μ = 0.4
- Distance to be covered, S = 400 m
- Initial velocity, u = 0 m/s (the car starts from rest)
- Final velocity, v = 0 m/s (the car comes to rest)
The maximum acceleration (a) of the car can be calculated using the formula:
a=μ⋅g
where g is the acceleration due to gravity (approximately 10m/s2).
a=0.4⋅10=4m/s2
Since the car accelerates to a certain speed and then decelerates back to rest, we can denote the time taken to accelerate as t and the time taken to decelerate as t as well (the times are equal for minimum time).
The distance covered during acceleration (S1) and deceleration (S2) can be expressed using the equation of motion:
S=ut+12at2
Since the initial velocity u=0:
S1=12at2(for acceleration)
S2=12at2(for deceleration)
S=S1+S2=12at2+12at2=at2
Setting this equal to the total distance of 400 m:
at2=400
Substituting a=4m/s2:
4t2=400
t2=4004=100
t=10s
Since the total time includes both the acceleration and deceleration phases:
Total time=t+t=10+10=20s
The minimum time in which the car can cover a distance of 400 m is 20 seconds.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples9videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.110videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
A block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionChoose the correct option:
A small collar of mass m is given an initial velocity of magnitude v0 on the horizontal circular track fabricated from a slender rod. If the coefficient of kinetic friction is μK, determine the distance traveled before the collar comes to rest. (Recognize that the friction force depends on the net normal force).
 View Solution
View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :
 View Solution
View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :
 View Solution
View SolutionThe coefficient of friction between the tyres and road is 0.4. The minimum distance covered before attaining a speed of 8ms−1 starting from rest is nearly ( take g=10ms−2)
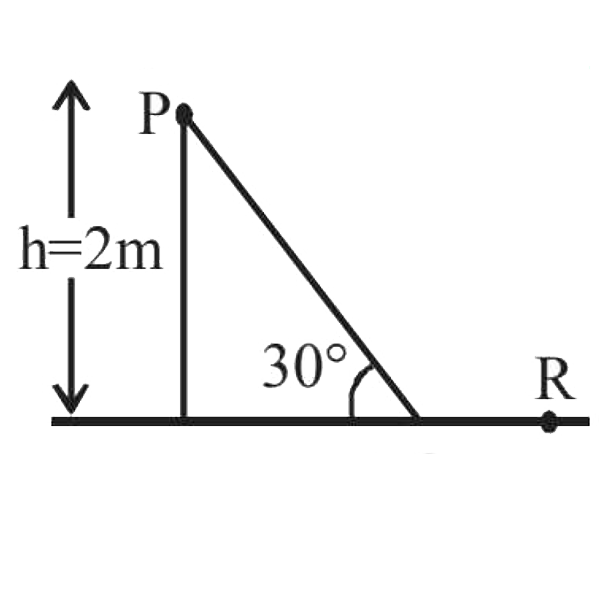
View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:
 View Solution
View SolutionA car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyres and the road is μ , the shortest distance in which the car can be stopped is
View SolutionA car, starting from rest, has a constant acceleration for a time interval t1 during which it covers a distance In the next time interval the car has a constant retardation and comes to rest after covering a distance in time Which of the following relations is correct?
View SolutionA car of mass m has an engine which can deliver power P. The minimum time in which car can be accelerated from rest to a speed v is :-
View SolutionA car of mass m has an engine which can deliver power P. The minimum time in which car can be accelerated from rest to a speed v is :-
View Solution

