In the figure shown tension in string always lies between and . <
Tension in massless string is uniform throughout. 
If both Accertion and Reason are true and the reason is correct explanation of the Assertion.
If both Assertion and Reason are true but reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:B
If
FBD of
:.
Since , but
Similarly, we can prove that
Therefore under all condition lines between and .
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct90videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question32videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.52videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
Find the value of tension in string 1 if the system equilibrium ? (g=10 m/s2)
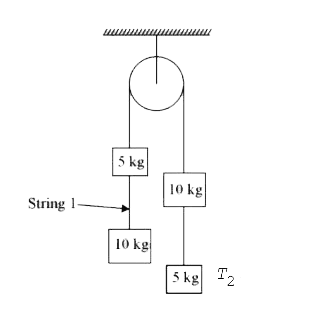 View Solution
View SolutionIn the figure, pulleys are smooth and strings are massless, m1=1 kg and m2=13kg. To keep m3 at rest, mass m3 should be
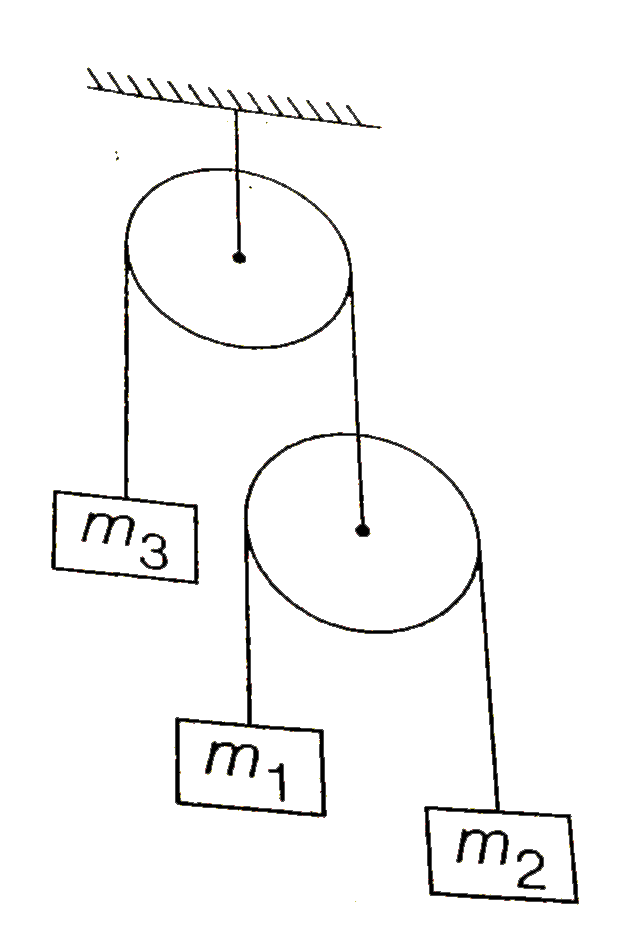 View Solution
View SolutionIn the figure shown , the tension is strings are T1 and T2 for figure (1) and (2) respectively and acceleration of mass m are a1 and a2 for figure (1) and (2) respectively.Select the correct option
View SolutionIn the arrangement shown in the figure the mass M is very heavy compared to m(M>>m). The tension T in the string suspende from the ceiling is
 View Solution
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
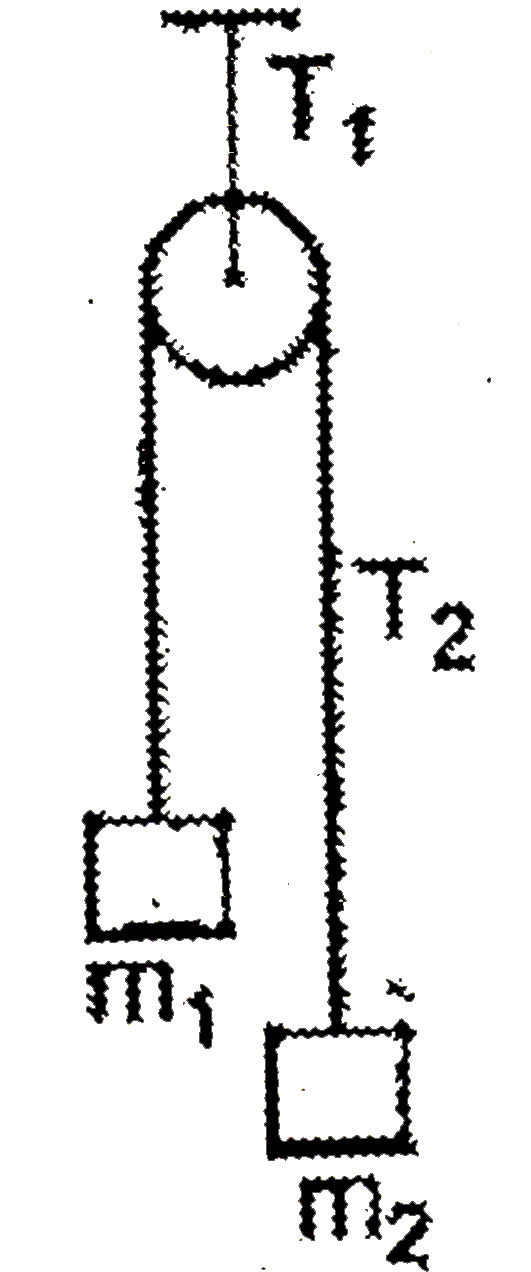
If m1=m2andm1 is moving at a certain instant with velocity v upward with respect to lift and the lift is moving in upward direction with constant acceleration (a<g) then speed of m2 with respect to lift :View SolutionIn the figure masses m1,m2 and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.View SolutionIn the figure shown , two blocks of masses 2 kg and 4kg are connected by a massless string which is just taut (i.e., tension is zero at this moment ). Now two forces 4 N and 15 N are applied on blocks . The tension in the string is (coefficient of static and kinetic friction are same ). [ g = m/s2]
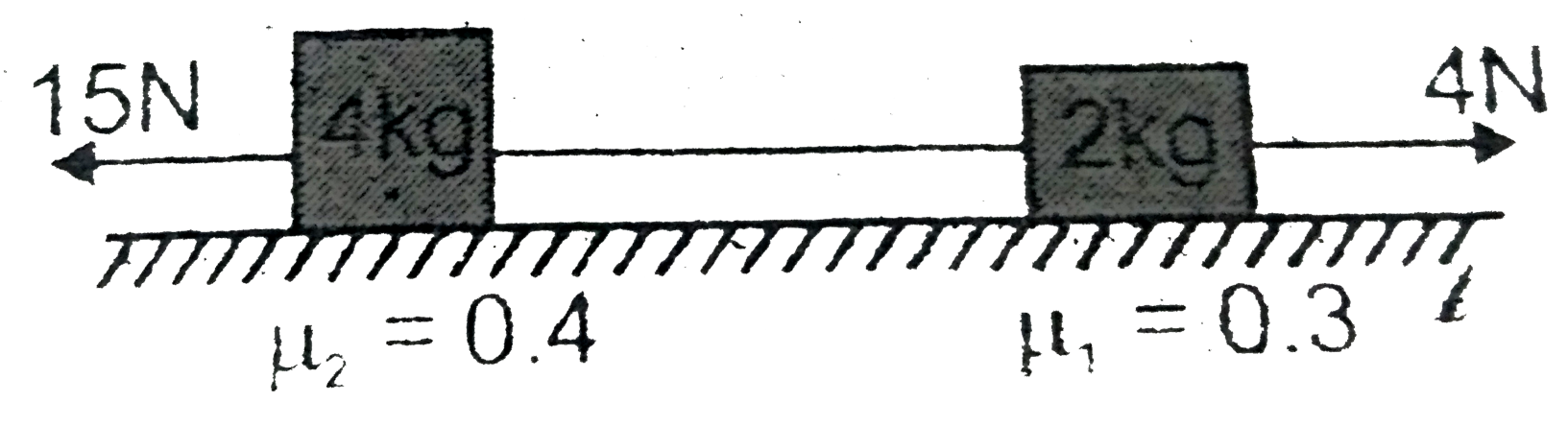 View Solution
View SolutionIn the following figure, if the tension in the string AB is 51N, then the tension in the string BC will be :-
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the stringView SolutionIf tension in string A and string B are TA and TB then find out TATB (assume that stringe are light and g=10m/s2) :
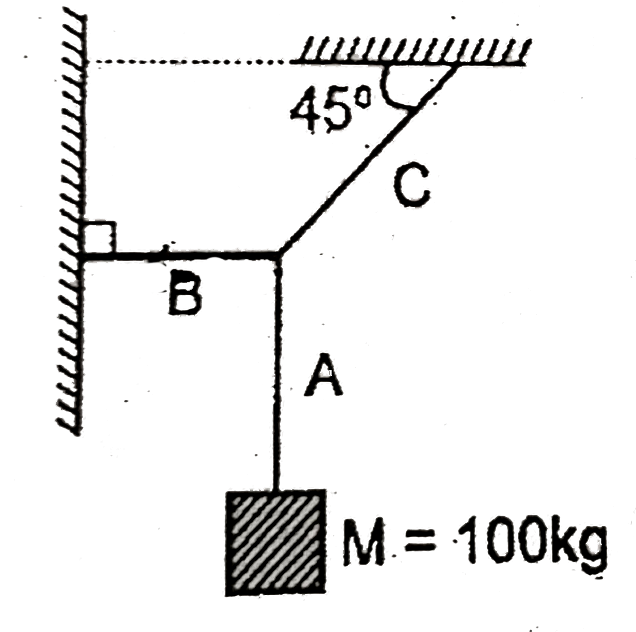 View Solution
View Solution

