In the figure shown , the tension is strings are T1 and T2 for figure (1) and (2) respectively and acceleration of mass m are a1 and a2 for figure (1) and (2) respectively.Select the correct option
T1>T2anda2>a1
T_2gtT_1 and a_1gta_2
T1>T2anda1>a2
T2>T1anda2>a1
The correct Answer is:C
To solve the problem, we need to analyze the two figures provided and derive the relationships between the tensions T1 and T2, and the accelerations a1 and a2.
Step 1: Analyze Figure 1
In Figure 1, we have a mass m connected to a pulley system. The forces acting on the mass are:
- The gravitational force acting downward: mg
- The tension in the string acting upward: T1
According to Newton's second law, the net force acting on the mass is equal to the mass times its acceleration:
T1−mg=ma1
Rearranging this gives:
T1=mg+ma1
Step 2: Analyze Figure 2
In Figure 2, we have a different configuration where a mass 2m is also connected to the pulley system. The forces acting on the mass 2m are:
- The gravitational force acting downward: 2mg
- The tension in the string acting upward: T2
Applying Newton's second law again:
T2−2mg=−2ma2
This indicates that the acceleration a2 is downward, hence the negative sign. Rearranging gives:
T2=2mg−2ma2
Step 3: Relate the Accelerations
From the analysis of both figures, we have two equations:
1. T1=mg+ma1
2. T2=2mg−2ma2
Step 4: Solve for the Accelerations
From the first equation, we can express a1:
a1=T1−mgm
From the second equation, we can express a2:
a2=2mg−T22m
Step 5: Compare the Tensions and Accelerations
To compare a1 and a2, we can analyze the relationship between T1 and T2.
From the equations we derived:
1. T1=mg+ma1
2. T2=2mg−2ma2
Since a1 is the acceleration of mass m upwards and a2 is the acceleration of mass 2m downwards, we can conclude that:
- If a1 is greater than a2, then T1 must be greater than T2.
Conclusion
From the analysis, we find that:
- a1>a2
- T1>T2
Thus, the correct option is:
Option C: T1>T2 and a1>a2.
In Figure 1, we have a mass m connected to a pulley system. The forces acting on the mass are:
- The gravitational force acting downward: mg
- The tension in the string acting upward: T1
T1−mg=ma1
Rearranging this gives:
T1=mg+ma1
In Figure 2, we have a different configuration where a mass 2m is also connected to the pulley system. The forces acting on the mass 2m are:
- The gravitational force acting downward: 2mg
- The tension in the string acting upward: T2
T2−2mg=−2ma2
This indicates that the acceleration a2 is downward, hence the negative sign. Rearranging gives:
T2=2mg−2ma2
From the analysis of both figures, we have two equations:
1. T1=mg+ma1
2. T2=2mg−2ma2
From the first equation, we can express a1:
a1=T1−mgm
a2=2mg−T22m
To compare a1 and a2, we can analyze the relationship between T1 and T2.
1. T1=mg+ma1
2. T2=2mg−2ma2
- If a1 is greater than a2, then T1 must be greater than T2.
From the analysis, we find that:
- a1>a2
- T1>T2
Option C: T1>T2 and a1>a2.
Similar Questions
Knowledge Check
In the shown in the given figure, the resistances R1andR2 are respectively
 A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
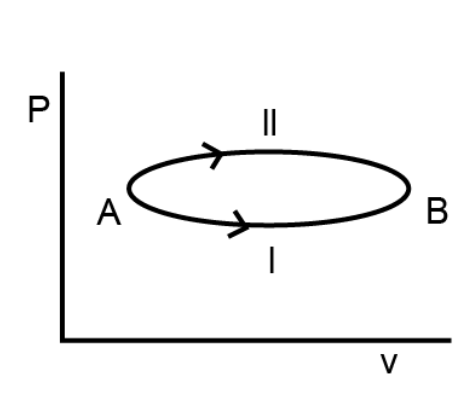
Two path 1 and 2 are shown in figure. If the change in internal energies are U, and U2 for path 1 and 2 respectively, then
View SolutionIn the figure shown tension in string AB always lies between m1g and m2g. (m1≠m2) <
Tension in massless string is uniform throughout.
View SolutionThe tension T in the string shown in figure is

View SolutionIn the arrangment shown in the figure, the ratio of tensions T1:T2:T3 is:

View SolutionShown in the figure is a system of three particles of mass 1kg,2kg and 4kg connected by two springs. The acceleration of A.B and C at any instant are 1ms−2,2ms−2 and 1/2ms−2 respectively directed as shown in the figure external force acting on the system is
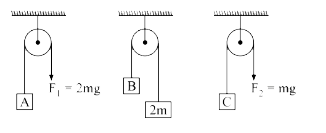
View SolutionIn the figure, blocks A, B and C of mass m each have acceleration a1, a2 and a3 respectively. F1 and F2 are external forces of magnitudes 2mg and mg respectively, then :
View SolutionIn the system shown in figure pully is smooth. Strings is massless and inextensible.Find acceleration of the system a, tension T1 andT2 (g=10m/s2)
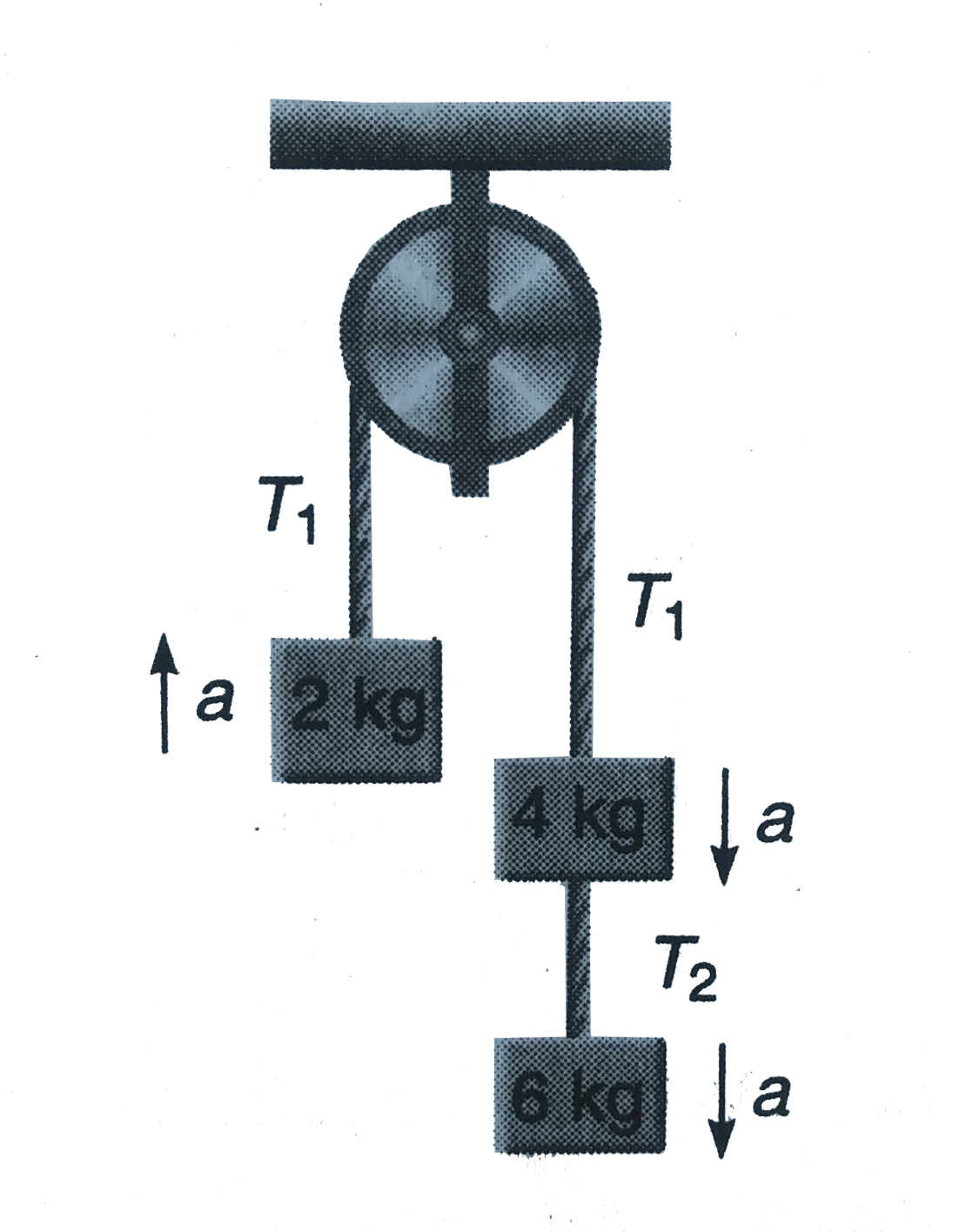
View Solution