Coefficient of friction between two block shown in figure ia μ=0.4. The blocks are given velocities of 2m/s and 8m/s in the directions figure. Find

(a) The time when relative motion between them will stop
(b) the common velocities of blocks upto that instant. (c) Displacement of 1kgand 2kg block upto that instant (g=10m/s2).
2kg block has relative motion towards right.Therefore , maximum friction will acts on it towards left
f=μN=(0.4)(1)(10)=4N
a1=41=4m/s2
a2=−42=2m/s2
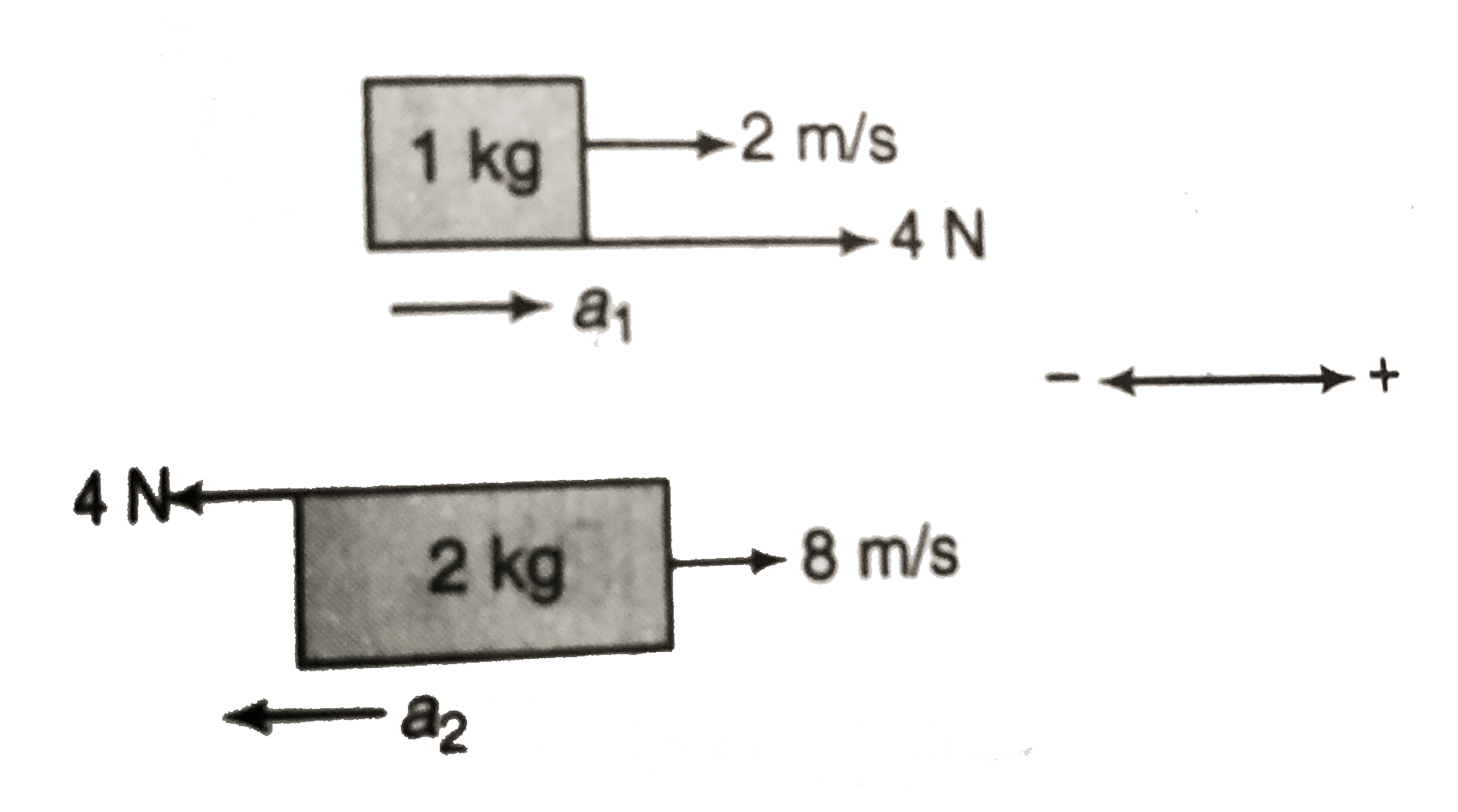
(b) Relative motion between them will stop when ,
v1=v1 ...(i)
∴u1+a1t=u2+a2t ...(ii)
∴2+4t=8−2t ...(iv) or t=1s
(b) Substituting value of 't' in Eq. (ii),either on RHS or on LHS common velocity =6m/s
( c) s1=u1t+12a1t2
=(2)(1)+12(4)(1)2=4m
s2=u2t+12a2t2
=(8)(1)+12(−2)(1)2=7m
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question32videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension9videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason28videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
coefficient of friction between two blocks shown in figure is μ=0.6. The blocks are given velocities in the direction shown in figure. Find
(a) the time when relative motion between them is stopped.
(b) the common velocity of the two blocks.
(c) the displacement of 1kg and 2kg blocks upto that instant. (Takeg=10m/s2)
 View Solution
View SolutionA conveyor belt is moving with constant speed of 6m/s. A small block is just dropped on it.Coefficient of friction between the two is μ=0.3. Find

(a) The time when relative motion between them will stop
(b) Displacement of block upto that instant (g=10m/s2).View SolutionThe coefficient of friction between the two blocks shown in the figure is μ=0.4 and between the lower block and the ground is zero. The blocks are given velocities of 2ms−1 and 8ms−1 respectively in the direction shown in the figure. In how much time (in seconds) the slipping between the blocks will stops ?
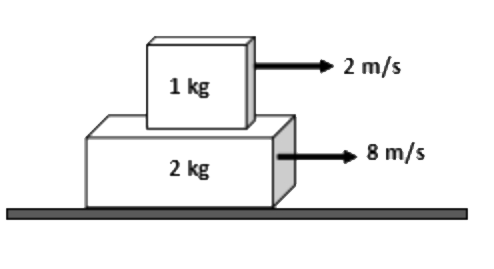 View Solution
View SolutionIn the figure shown, upper block is given a velocity of 6m/s and lower block. 3m/s. When relative motion between them is stopped
 View Solution
View SolutionIn the figure shown, upper block is given a velocity of 6m/s and lower block. 3m/s. When relative motion between them is stopped
 View Solution
View SolutionIn the arrangement shown, velocity of block A is 10 m/s at a moment. Then the velocity of block B at this instant is :
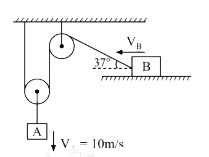 View Solution
View Solution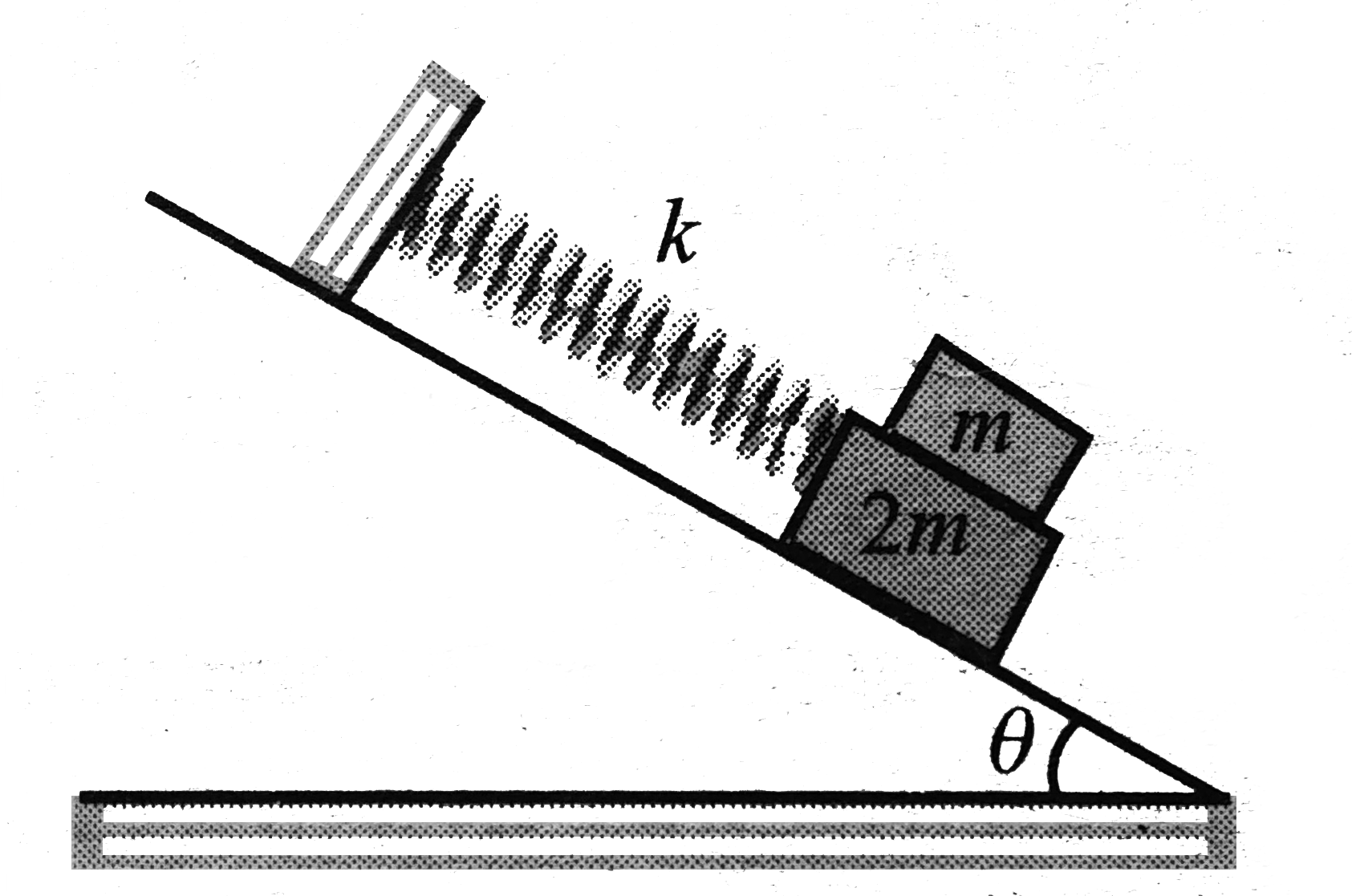
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks isView Solution
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks isView SolutionThe friction coefficient between the horizontal surfce and ech of the blocks shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g=10ms2.
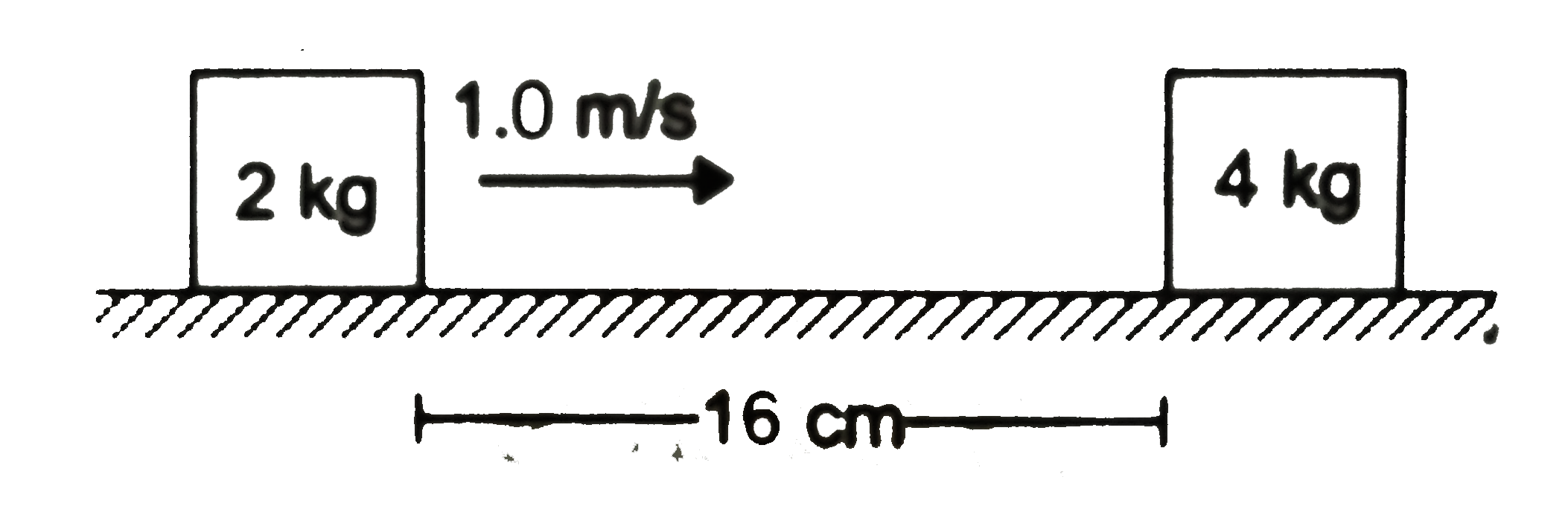 View Solution
View SolutionTwo blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
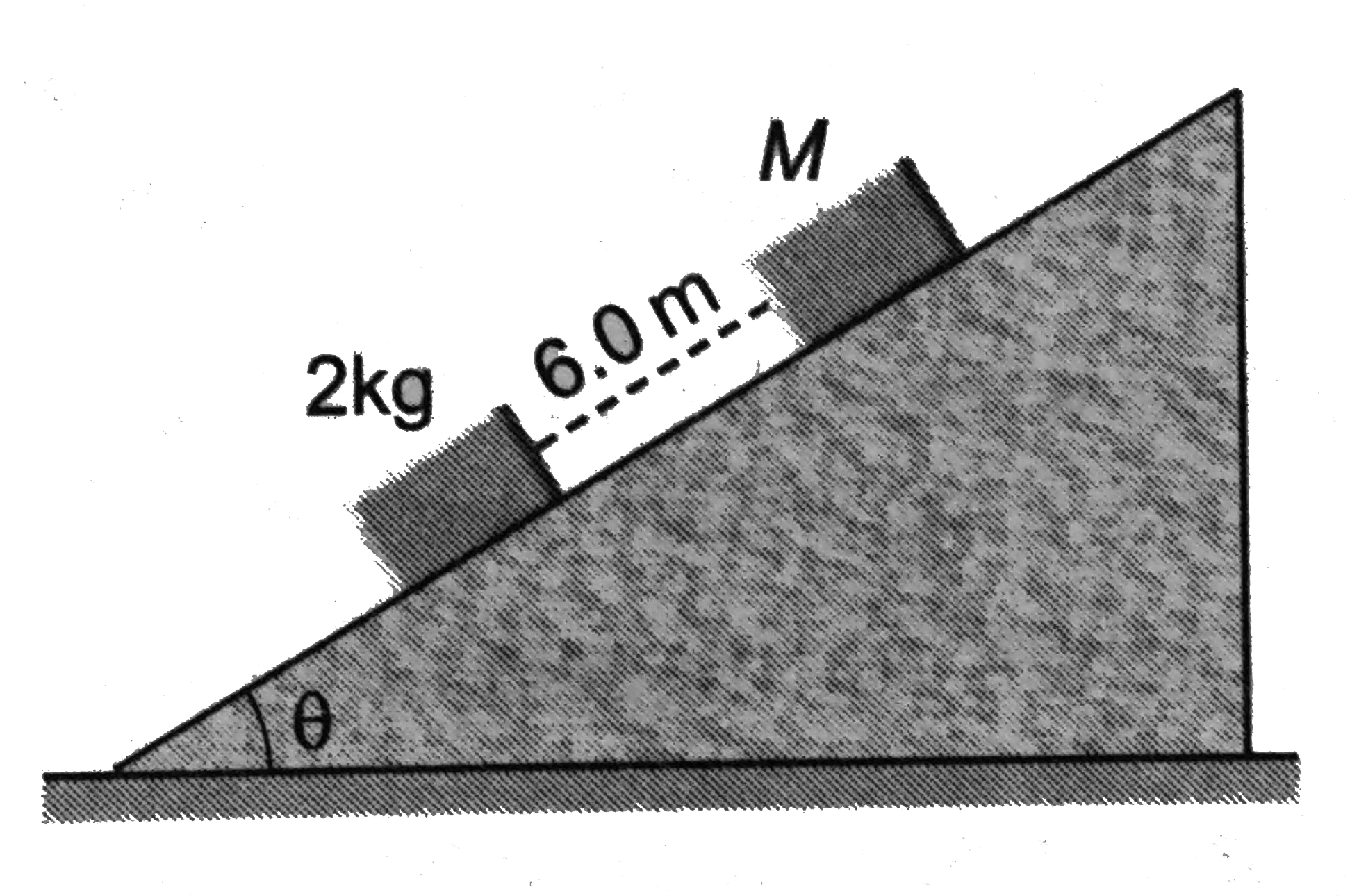 View Solution
View Solution

