The upper portion of an inclined plane of inclination a is smooth and the lower portion is rough. A partical slide down from rest the top and just comes to rest at the foot . If the ratio of smooth length to rough length is m:n, find the coefficient of friction .
To solve the problem step by step, we need to analyze the motion of the particle on the inclined plane, which consists of a smooth upper portion and a rough lower portion.
Step 1: Define the problem
Let the length of the smooth portion of the inclined plane be S1=m and the length of the rough portion be S2=n. The angle of inclination is α.
Step 2: Apply the equations of motion
Since the particle starts from rest and comes to rest at the foot of the incline, we can use the equations of motion.
For the smooth portion:
- Initial velocity u=0
- Final velocity v (at the end of the smooth portion)
- Acceleration a1=gsinα (due to gravity)
Using the equation:
v2=u2+2a1S1
we get:
v2=0+2(gsinα)(m)=2mgsinα
For the rough portion:
- Initial velocity u=v (the velocity at the end of the smooth portion)
- Final velocity v=0 (comes to rest)
- Acceleration a2=−μgcosα−gsinα (deceleration due to friction and gravity)
Using the equation:
0=v2+2a2S2
we can substitute v2 from the smooth portion:
0=2mgsinα+2(−μgcosα−gsinα)(n)
Step 3: Rearranging the equation
This simplifies to:
0=2mgsinα−2n(μgcosα+gsinα)
Dividing through by 2g:
0=msinα−n(μcosα+sinα)
Step 4: Solve for the coefficient of friction μ
Rearranging gives:
msinα=n(μcosα+sinα)
msinα=nμcosα+nsinα
msinα−nsinα=nμcosα
(m−n)sinα=nμcosα
Thus, we can solve for μ:
μ=(m−n)sinαncosα
Step 5: Final expression for μ
This can be rewritten using the tangent function:
μ=(m−n)ntanα
Conclusion
The coefficient of friction μ is given by:
μ=(m−n)ntanα
Let the length of the smooth portion of the inclined plane be S1=m and the length of the rough portion be S2=n. The angle of inclination is α.
Since the particle starts from rest and comes to rest at the foot of the incline, we can use the equations of motion.
- Initial velocity u=0
- Final velocity v (at the end of the smooth portion)
- Acceleration a1=gsinα (due to gravity)
v2=u2+2a1S1
we get:
v2=0+2(gsinα)(m)=2mgsinα
- Initial velocity u=v (the velocity at the end of the smooth portion)
- Final velocity v=0 (comes to rest)
- Acceleration a2=−μgcosα−gsinα (deceleration due to friction and gravity)
0=v2+2a2S2
we can substitute v2 from the smooth portion:
0=2mgsinα+2(−μgcosα−gsinα)(n)
This simplifies to:
0=2mgsinα−2n(μgcosα+gsinα)
Dividing through by 2g:
0=msinα−n(μcosα+sinα)
Rearranging gives:
msinα=n(μcosα+sinα)
msinα=nμcosα+nsinα
msinα−nsinα=nμcosα
(m−n)sinα=nμcosα
Thus, we can solve for μ:
μ=(m−n)sinαncosα
This can be rewritten using the tangent function:
μ=(m−n)ntanα
The coefficient of friction μ is given by:
μ=(m−n)ntanα
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.120videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.215videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension9videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
The upper half of an inclined plane with an angle of inclination theta, is smooth while the lower half is rough. A body starting from rest at the top of the inclined plane comes to rest at the bottom of the inclined plane. Then the coefficient of friction for the lower half is
View SolutionThe upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionThe upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionThe upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionThe upper half of an inclined plane of inclination θ is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by
View SolutionThe upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionA block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
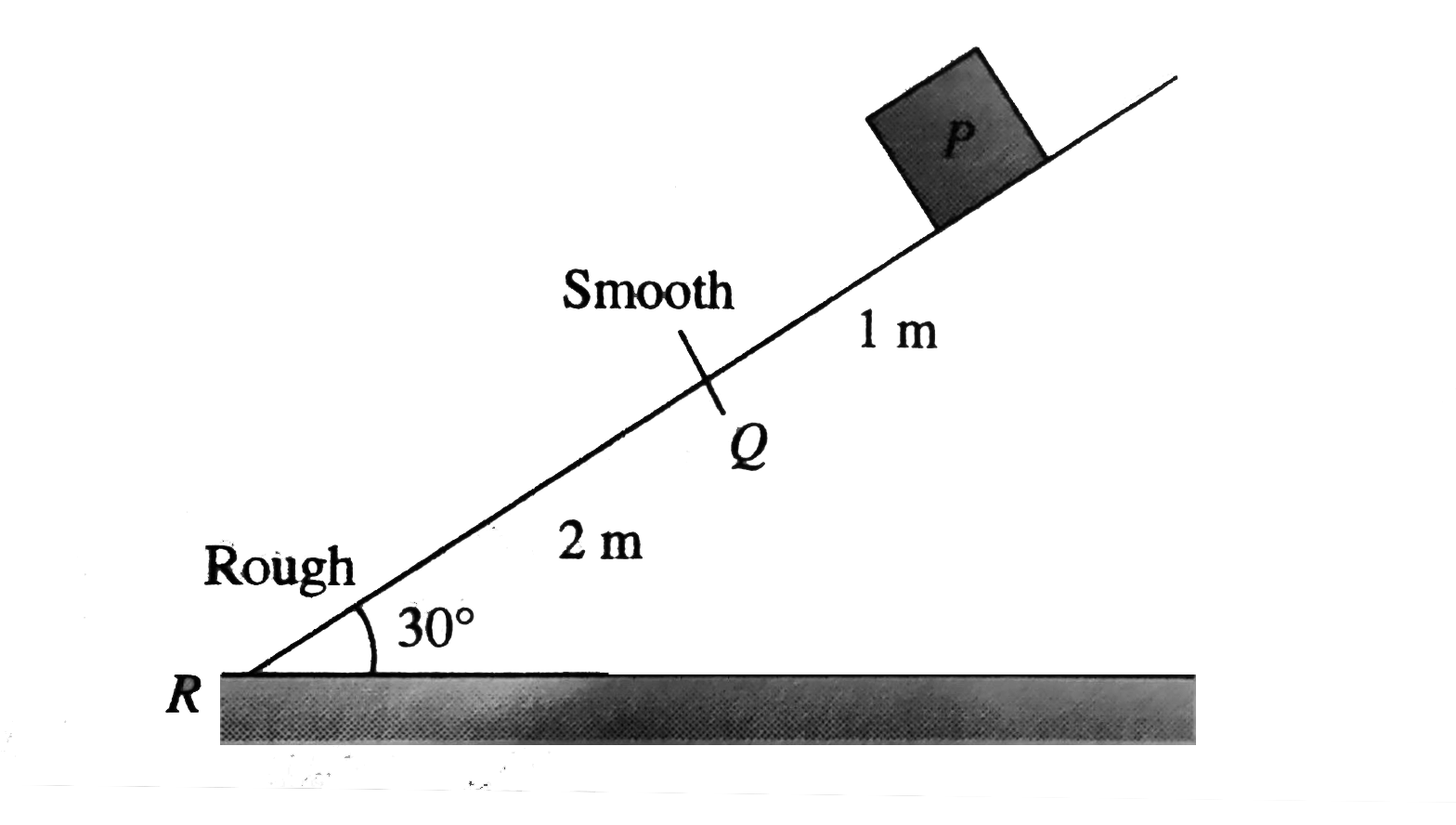 View Solution
View SolutionA block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
View SolutionA body takes 1(13) times as much time to slide down a rough inclined plane as it takes to slide down an identical bust smooth inclined plane. If the angle of inclination is 45°, find the coefficient of friction.
View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View Solution

