
A body of mass m, radius R and moment of inertia I (about an axis passing through the centre of mass and perpendicular to plane of motion) is released from rest over a sufficiently rough ground (to provide accelerated pure rolling) find linear acceleration of the body.
Let linear acceleration is a and angular acceleration α for accelerated pure rolling
α=aR
After time t, displacement of centre of mass along the plane s=12at2
∴ height fallen by centre of mass along the plane s=12at2
∴ height fallen by centre of mass
h=(s)(sinθ)=12at2sinθ
Linear velocity v=at
angular velocity ω=αt=atR
From energy conservation principle, decrease in potential energy = increase in translational and rotaional kinetic energy
or mgh=12mv2+12Iω2
Substituting the value we have
mg(12at2sinθ)=12m(at)2+12I(atR)2
Solving this equation we get a=gsinθ1+ImR2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown
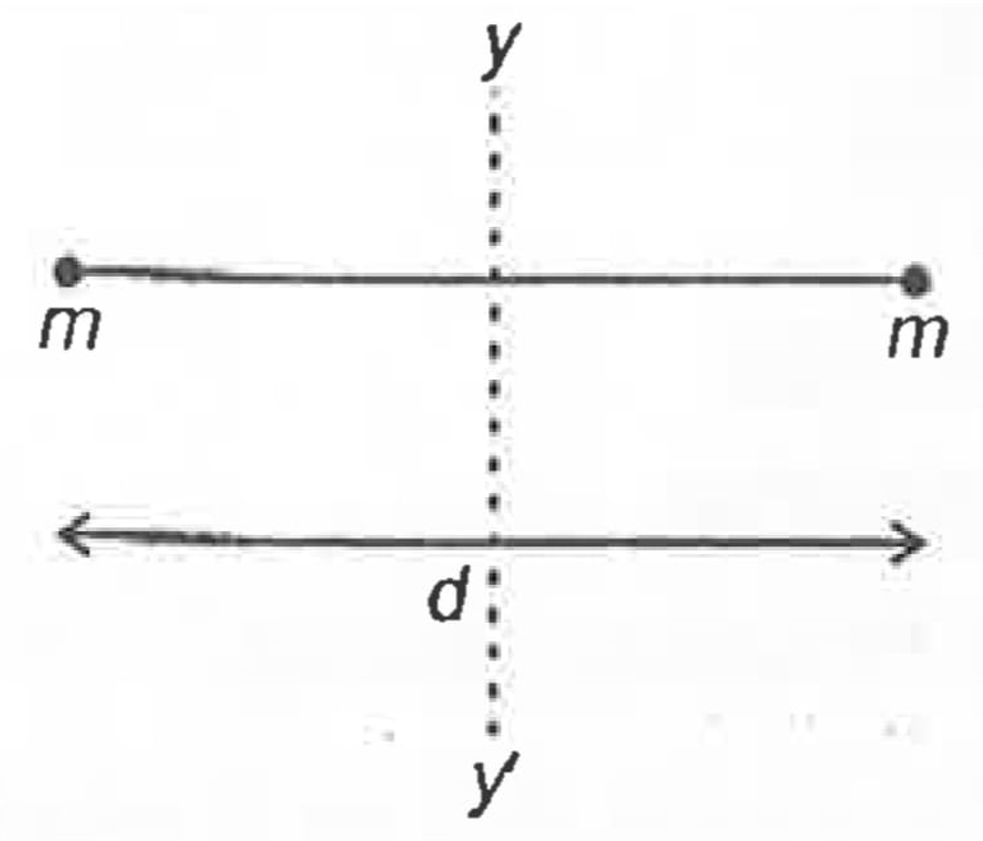
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionFor the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
View SolutionA uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View SolutionIn the given figure F=10N,R=1m, mass of the body is 2kg and moment of inertia of the body about an axis passing through O and perpendicular to the plane of the body is 4kgm2. O is the centre of mass of the body.

If the ground is sufficiently rough to ensure rolling, what is the kinetic energy of the body now in the given time interval of 2s?
View Solution
