In the figure given in the text if mass of the rod is m then find hinge force.
(a). Just after the rod is released from the horizontal position.
(b). When rod becomes vertical
To solve the problem of finding the hinge force on a rod of mass m at two different positions (just after it is released from the horizontal position and when it becomes vertical), we will break down the solution into two parts.
Part (a): Hinge Force Just After the Rod is Released from the Horizontal Position
1. Identify Forces Acting on the Rod:
- The weight of the rod mg acts downward at its center of mass, which is at a distance L2 from the hinge.
- The hinge exerts a force R on the rod, which has both vertical and horizontal components.
2. Calculate Torque:
- The torque τ about the hinge due to the weight of the rod is given by:
τ=mg⋅L2
- This torque will cause the rod to rotate.
3. Relate Torque to Angular Acceleration:
- The moment of inertia I of the rod about the hinge is:
I=13mL2
- Using Newton's second law for rotation:
τ=Iα⟹mg⋅L2=13mL2α
- Solving for angular acceleration α:
α=3g2L
4. Calculate Linear Acceleration of the Center of Mass:
- The tangential acceleration at of the center of mass is:
at=α⋅L2=3g2L⋅L2=3g4
5. Balance Forces in the Vertical Direction:
- The net force in the vertical direction is:
Ry−mg=ma
- Here, a is the acceleration of the center of mass:
Ry−mg=m⋅3g4
- Rearranging gives:
Ry=mg+3mg4=7mg4
6. Horizontal Forces:
- Initially, there is no horizontal motion, so the horizontal component of the hinge force Rx=0.
7. Total Hinge Force:
- The total hinge force R is:
R=√R2x+R2y=√0+(7mg4)2=7mg4
Part (b): Hinge Force When the Rod Becomes Vertical
1. Energy Conservation:
- The change in potential energy as the rod falls from horizontal to vertical is:
ΔPE=mg⋅L2
- This potential energy converts into kinetic energy:
ΔKE=12Iω2
- Substituting for I:
ΔKE=12⋅13mL2ω2
2. Setting Potential Energy Equal to Kinetic Energy:
- Equating the two:
mg⋅L2=16mL2ω2
- Solving for ω2:
ω2=3gL
3. Calculate Forces When Vertical:
- In the vertical position, the forces acting on the rod are:
- Weight mg acting downward.
- The hinge force R acting upward and horizontally.
4. Centripetal Force:
- The centripetal force required for the circular motion of the center of mass is:
Fc=m⋅L2⋅ω2=m⋅L2⋅3gL=3mg2
5. Vertical Force Balance:
- The vertical force balance gives:
R−mg=3mg2
- Rearranging gives:
R=mg+3mg2=5mg2
6. Horizontal Forces:
- The horizontal component of the hinge force is equal to the centripetal force:
Rx=3mg2
7. Total Hinge Force:
- The total hinge force when the rod is vertical is:
R=√R2x+R2y=√(3mg2)2+(5mg2)2=√9m2g24+25m2g24=√34m2g24=√342mg
Summary of Results:
- Hinge Force Just After Release: R=7mg4
- Hinge Force When Vertical: R=5mg2
- The weight of the rod mg acts downward at its center of mass, which is at a distance L2 from the hinge.
- The hinge exerts a force R on the rod, which has both vertical and horizontal components.
- The torque τ about the hinge due to the weight of the rod is given by:
τ=mg⋅L2
- This torque will cause the rod to rotate.
- The moment of inertia I of the rod about the hinge is:
I=13mL2
- Using Newton's second law for rotation:
τ=Iα⟹mg⋅L2=13mL2α
- Solving for angular acceleration α:
α=3g2L
- The tangential acceleration at of the center of mass is:
at=α⋅L2=3g2L⋅L2=3g4
- The net force in the vertical direction is:
Ry−mg=ma
- Here, a is the acceleration of the center of mass:
Ry−mg=m⋅3g4
- Rearranging gives:
Ry=mg+3mg4=7mg4
- Initially, there is no horizontal motion, so the horizontal component of the hinge force Rx=0.
- The total hinge force R is:
R=√R2x+R2y=√0+(7mg4)2=7mg4
- The change in potential energy as the rod falls from horizontal to vertical is:
ΔPE=mg⋅L2
- This potential energy converts into kinetic energy:
ΔKE=12Iω2
- Substituting for I:
ΔKE=12⋅13mL2ω2
- Equating the two:
mg⋅L2=16mL2ω2
- Solving for ω2:
ω2=3gL
- In the vertical position, the forces acting on the rod are:
- Weight mg acting downward.
- The hinge force R acting upward and horizontally.
- The centripetal force required for the circular motion of the center of mass is:
Fc=m⋅L2⋅ω2=m⋅L2⋅3gL=3mg2
- The vertical force balance gives:
R−mg=3mg2
- Rearranging gives:
R=mg+3mg2=5mg2
- The horizontal component of the hinge force is equal to the centripetal force:
Rx=3mg2
- The total hinge force when the rod is vertical is:
R=√R2x+R2y=√(3mg2)2+(5mg2)2=√9m2g24+25m2g24=√34m2g24=√342mg
- Hinge Force Just After Release: R=7mg4
- Hinge Force When Vertical: R=5mg2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Two particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:

View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.

View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass in is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical.

View SolutionA uniform rod of length 75cm is hinged at one of its ends and is free to rotate in vertical plane. It is released from rest when rod is horizontal. When the rod becomes vertical, it is breaks at mid− point and lower part now moves freely. The distance of centre of lower part from hinge, when it again becomes vertical for the first time is r. Find the approximate value of 2r.
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionA light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the
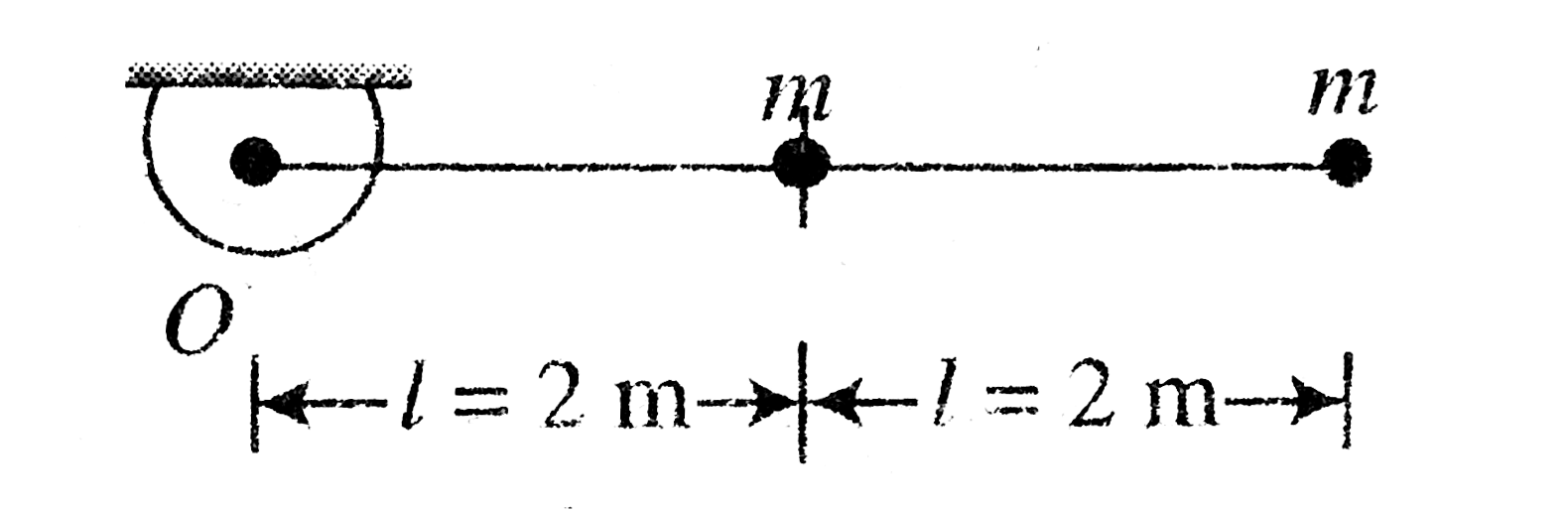
reaction offered by the pivot at t=0 (in N).
View SolutionA simple pendulum A and a homogeneous rod B hinged at its enda are released from horizontal position as shown in figure.

View SolutionA uniform rod AB of mass 3m and length 4l, which is free to turn in a vertical plane about a smooth horizontal axis through A, is released from rest when horizontal. When the rod first becomes vertical, a point C of the rod, where AC=3l strikes a fixed peg. Find the linear impulse exerted by the peg on the rod if
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle π3 radian.
View Solution
