A cube is resting on an inclinded plane. If the angle of inclination is gradually increased. What must be the coefficient of friction between the cube and plane so that,
(a). Cube slides before toppling?
(b). Cube topples before sliding?
To solve the problem of determining the coefficient of friction between a cube and an inclined plane such that the cube either slides before toppling or topples before sliding, we can analyze the forces and torques acting on the cube.
Step 1: Identify Forces Acting on the Cube
When the cube is resting on the inclined plane at an angle θ, the following forces act on it:
- Weight (mg) acting vertically downward.
- Normal force (N) acting perpendicular to the inclined plane.
- Frictional force (F) acting parallel to the inclined plane, opposing the motion.
Step 2: Resolve the Weight into Components
The weight of the cube can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
Step 3: Condition for Sliding Before Toppling
For the cube to slide before toppling, the force causing sliding (which is mgsinθ) must be greater than the maximum static frictional force (which is F=μN):
mgsinθ>F
Since the normal force N is equal to mgcosθ, we can substitute:
mgsinθ>μ(mgcosθ)
Dividing both sides by mg (assuming mg≠0):
sinθ>μcosθ
Dividing both sides by cosθ:
tanθ>μ
Thus, for the cube to slide before toppling, the coefficient of friction must satisfy:
μ<tanθ
Step 4: Condition for Toppling Before Sliding
For the cube to topple before sliding, we need to analyze the torques about the edge of the cube that is in contact with the inclined plane. The torque due to the normal force (N) must be greater than the torque due to the frictional force (F).
The torque due to the normal force about the edge is:
τN=N⋅a2
The torque due to friction is:
τF=F⋅a2
Setting these two torques equal for rotational equilibrium:
N⋅a2=F⋅a2
This simplifies to:
N=F
Substituting F=μN:
N=μN
For this to hold true, we must have:
μ>1
Thus, for the cube to topple before sliding, the coefficient of friction must satisfy:
μ>1
Final Results:
(a) The condition for the cube to slide before toppling is:
μ<tanθ
(b) The condition for the cube to topple before sliding is:
μ>1
When the cube is resting on the inclined plane at an angle θ, the following forces act on it:
- Weight (mg) acting vertically downward.
- Normal force (N) acting perpendicular to the inclined plane.
- Frictional force (F) acting parallel to the inclined plane, opposing the motion.
The weight of the cube can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
For the cube to slide before toppling, the force causing sliding (which is mgsinθ) must be greater than the maximum static frictional force (which is F=μN):
mgsinθ>F
Since the normal force N is equal to mgcosθ, we can substitute:
mgsinθ>μ(mgcosθ)
Dividing both sides by mg (assuming mg≠0):
sinθ>μcosθ
Dividing both sides by cosθ:
tanθ>μ
Thus, for the cube to slide before toppling, the coefficient of friction must satisfy:
μ<tanθ
For the cube to topple before sliding, we need to analyze the torques about the edge of the cube that is in contact with the inclined plane. The torque due to the normal force (N) must be greater than the torque due to the frictional force (F).
τN=N⋅a2
The torque due to friction is:
τF=F⋅a2
N⋅a2=F⋅a2
This simplifies to:
N=F
Substituting F=μN:
N=μN
For this to hold true, we must have:
μ>1
Thus, for the cube to topple before sliding, the coefficient of friction must satisfy:
μ>1
(a) The condition for the cube to slide before toppling is:
μ<tanθ
μ>1
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform cylinder of height h and radius r is placed with its circular face on a rough inclined plane and the inclination of the plane to the horizontal is gradually increased. If μ is the coefficient of friction, then under what condition the cylinder will (a) slide before toppling (b) topple before sliding.
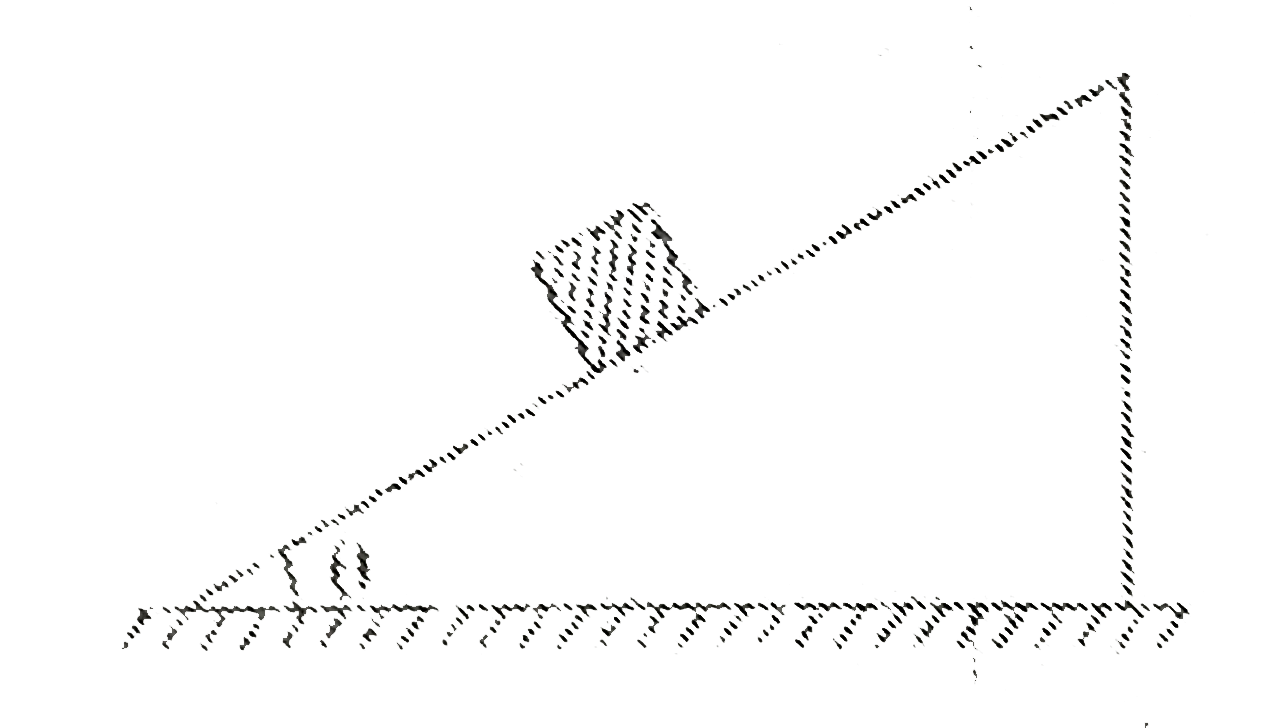
View SolutionA cube is pplaced on an inclined plane of inclinbation θ as shown in figure. Cofficent of friction br=etween the cube and the plane is μ. As the angle θ is gradually increased, the cube slides before toppling if
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA piece of ice slides down a 45∘ incline in twice the time it takes to slide down a frictionless 45∘ incline . What is the coefficient of friction between the ice and the incline ? .
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA wooden block is placed on an inclined plane. The block just begins to slide down when the angle of the inclination is increased to 45°. What is the coefficient of the friction?
View SolutionA block is pushed up a rough inclined plane of 45°. If the time of descent is twice the time of ascent, the coefficient of friction is
View SolutionA block of dimensions a×a×2a is kept on an inclined plane of inclination 37∘. The longer side is perpendicular to the plane. The co− efficient of friction between the block and the plane is 0.8. By numerical analysis find whether the block will topple or not.
View SolutionAn ice cube is kept on an inclined plane of angle 30∘. The coefficient to kinetic friction between the block and incline plane is the 1/√3. What is the acceleration of the block ?
View Solution
