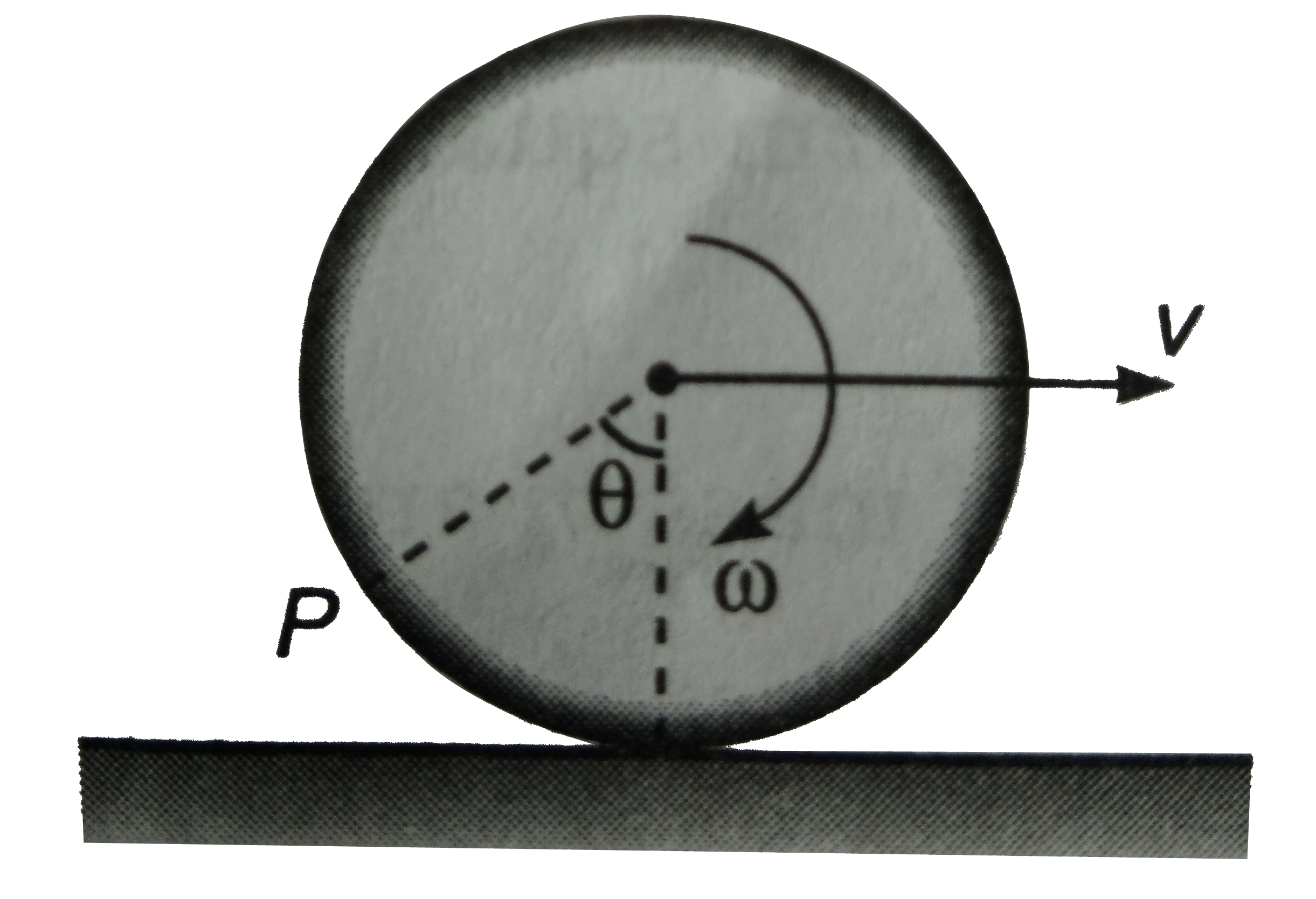
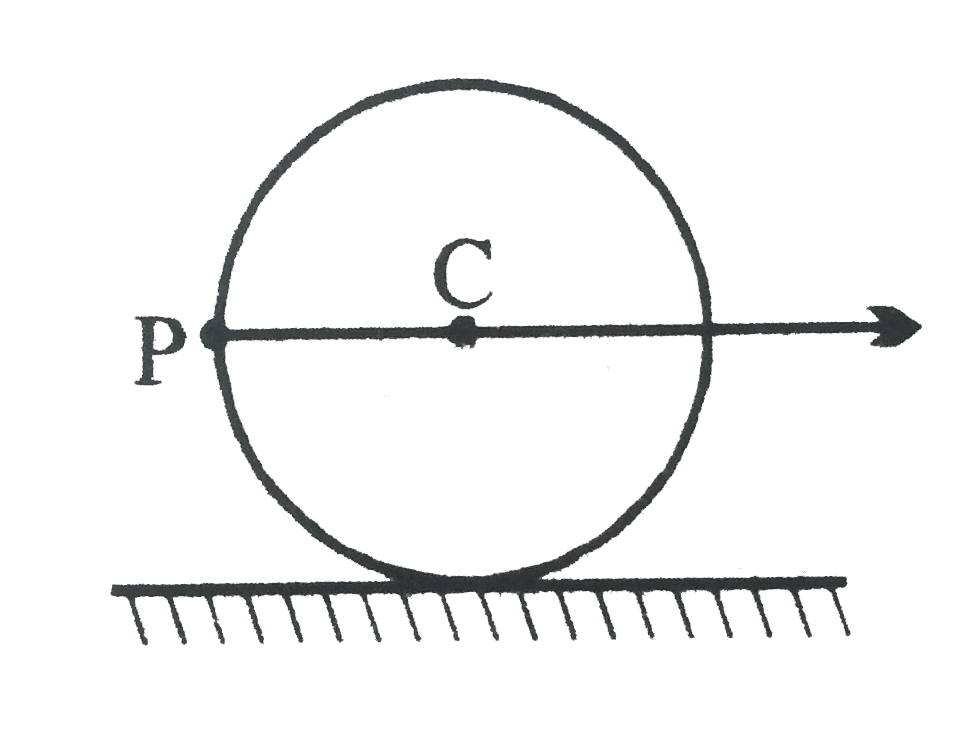
A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of θ the velocity of point P is in vertical direction (v<Rω).

If Rωcosθ= then velocity of point P is vertically upwards
θ=±cos−1(vRω)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Choose the correct option:
A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
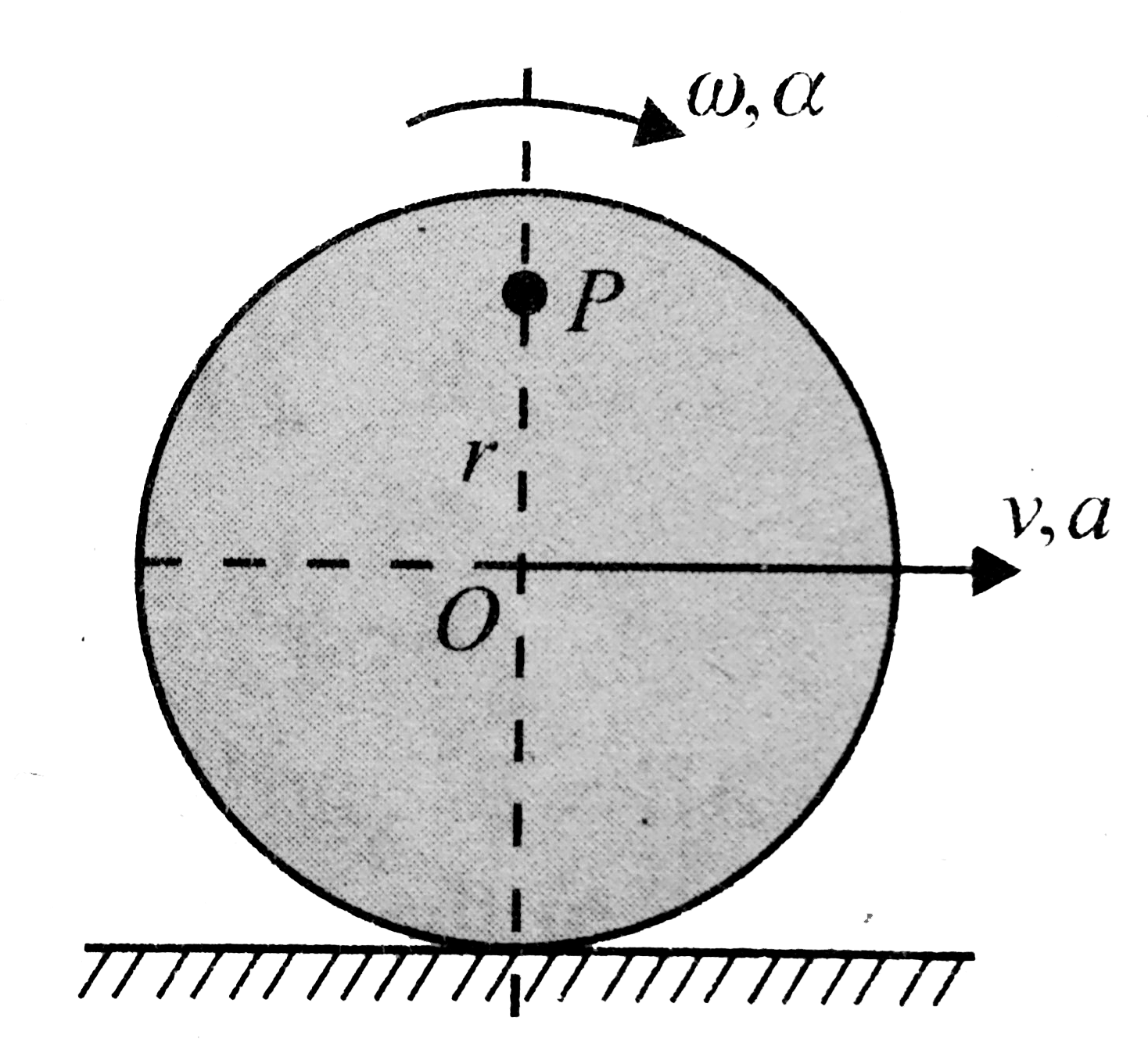
View SolutionA disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in figure. The magnitude of acceleration of point P at an instant when its linear velocity is v and angular velocity is ω will be:

View SolutionA hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
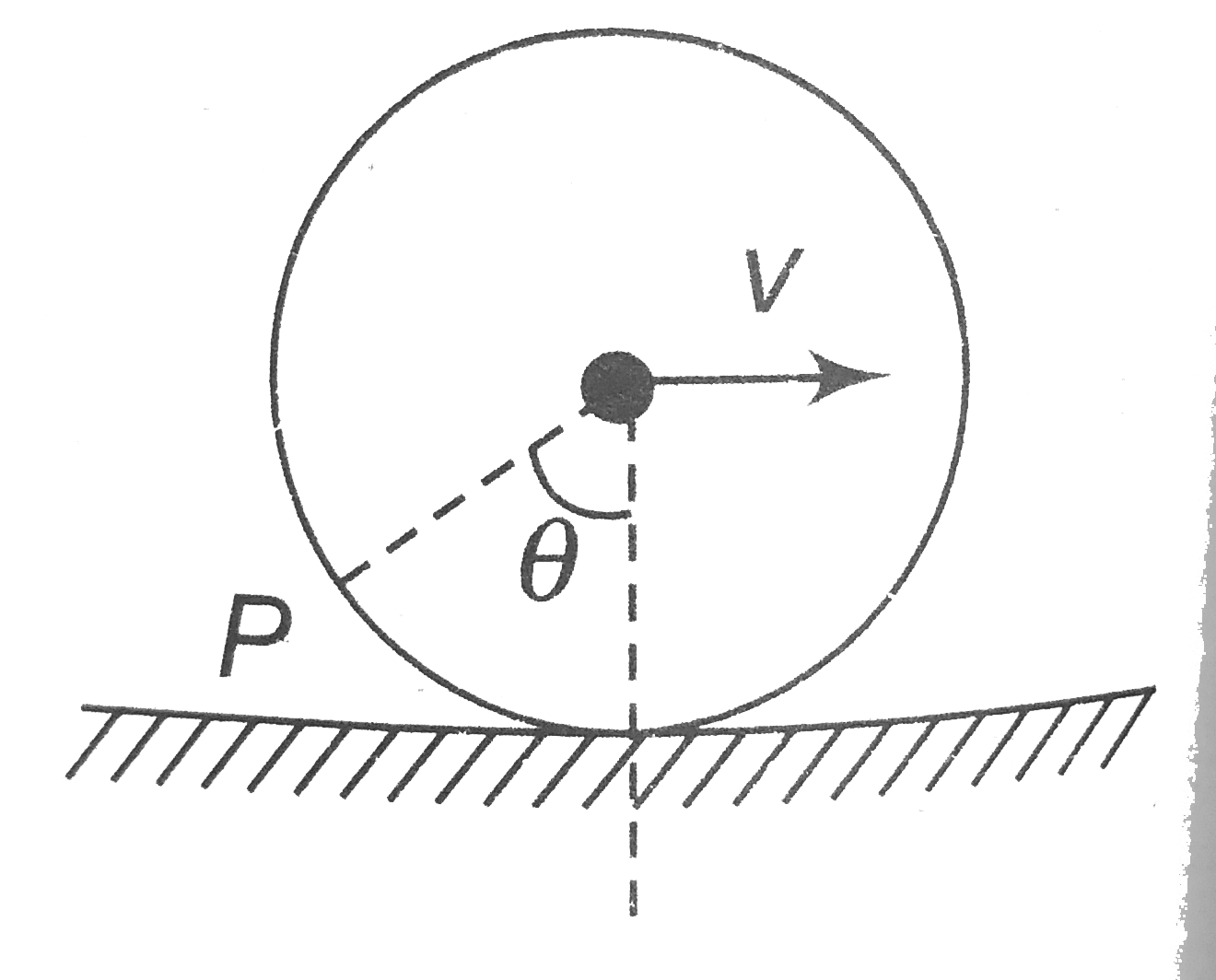
View SolutionA disc of radius R start at time t=0 moving along the positive X-axis with linear speed v and angular speed ω. Find the x and y-coordinates of the bottommost point at any time t.

View SolutionA disc of radius R starts at time t=0 moving along the positive x-axis with linear speed v and angular speed ω. Find the x and y coordinates of the bottom most poitn at any time t.
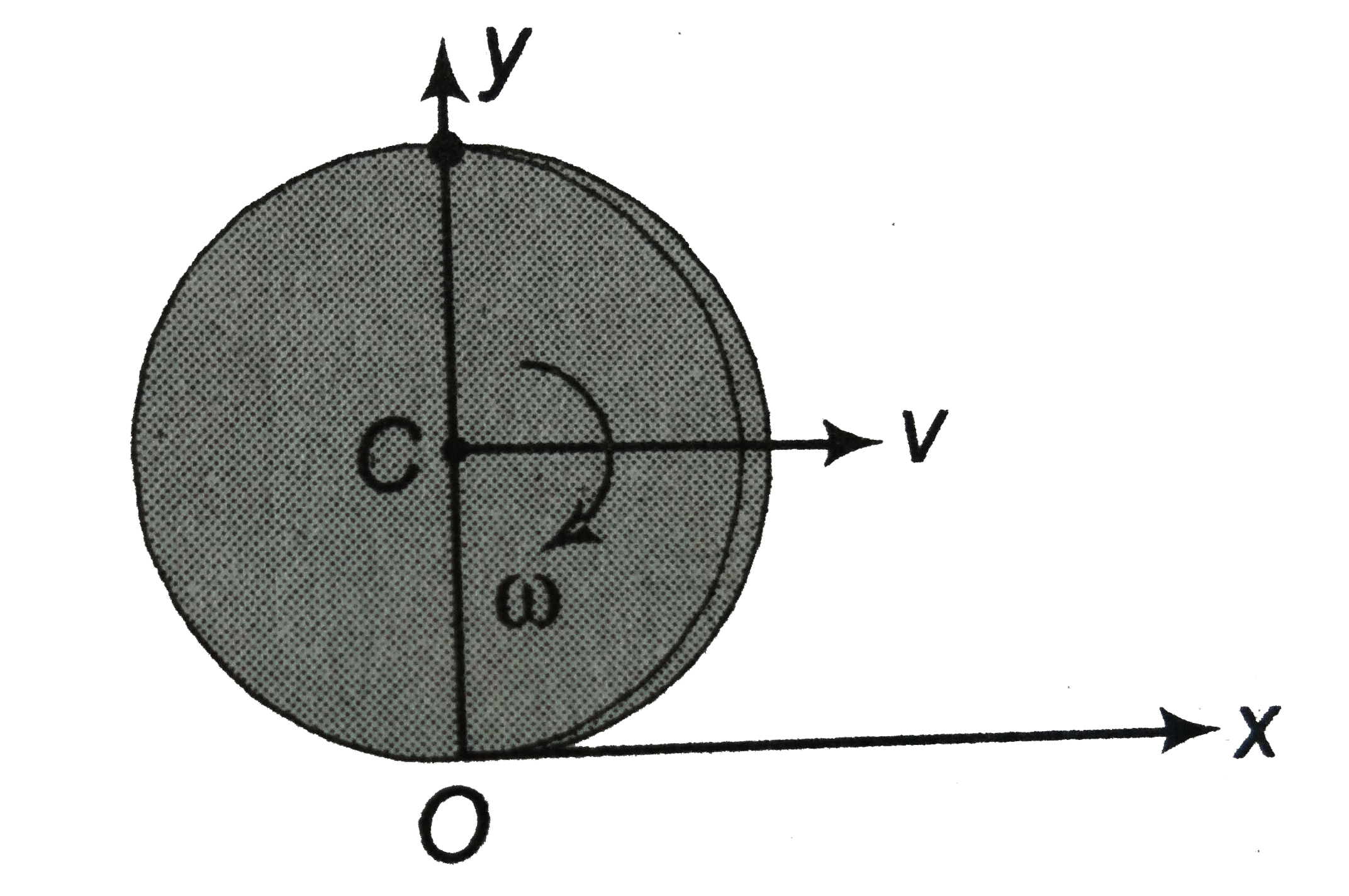
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v0 as shown in the figure. For what value of θ, speed of point P will be v02√(5+2√3) ? (OP= R/2 and O is the centre of disc)

View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point P is

View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
 .
.
View Solution
