
The figure shows a thin ring of mass M=1kg and radius R=0.4m spinning about a vertical diameter (take I=12MR2) A small beam of mass m=0.2kg can slide without friction along the ring When the bead is at the top of the ring the angular velocity is 5rad/s What is the angular velocity when the bead slips halfwat to θ=45∘?
I1ω1=I2ω2
∴ω2=(I1I2)ω1
=(12MR2)[12MR2+m(R√2)2]ω1
=(MM+m)ω1=(11+0.2)5
=256rad/s
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct26videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct36videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective30videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad/s. What is angular velocity (in rad/s) if a mass of 0.5 kg is put on the circumference of the disc ?
View SolutionA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc ?
View SolutionA thin ring of mass 2kg and radius 0.5 m is rolling without on a horizontal plane with velocity 1m/s. A small ball of mass 0.1kg, moving with velocity 20 m/s in the opposite direction hits the ring at a height of 0.75m and goes vertically up with velocity 10m/s. Immediately after the collision
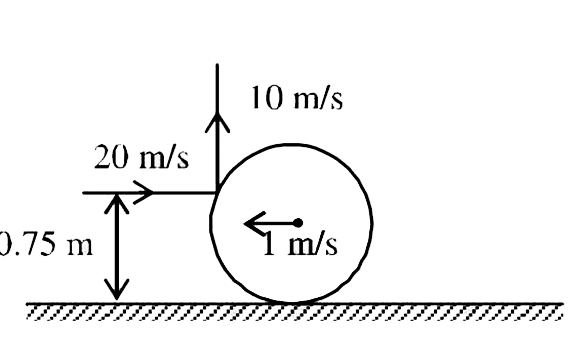 View Solution
View SolutionA disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc?
View SolutionCalculate the magnitude of linear acceleration of a particle moving in a circle of radius 0.5 m at the instant when its angular velocity is 2.5 rad s–1 and its angular acceleration is 6rads−2.
View SolutionCalculate the magnitude of linear acceleration of a particle moving in a circle of radius 0.5 m at the instant when its angular velocity is 2.5 rad s–1 and its angular acceleration is 6rads−2.
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
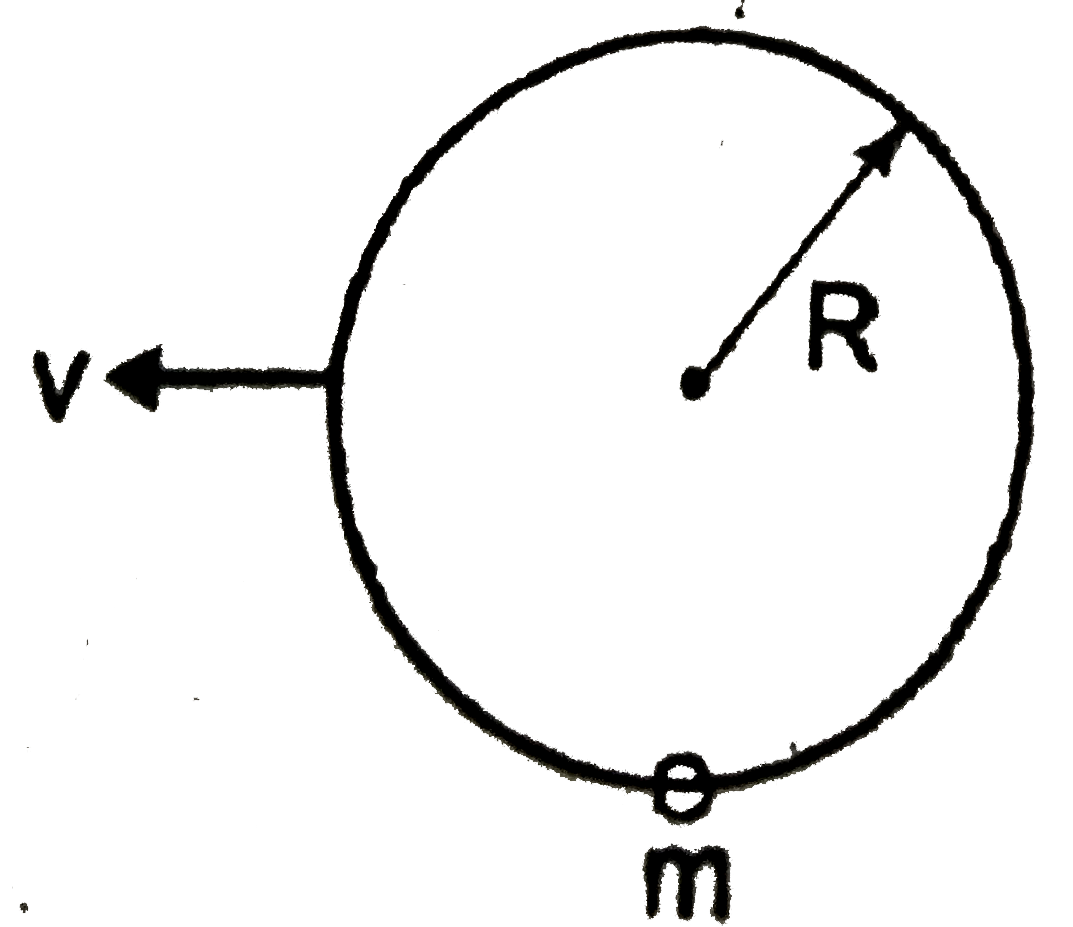 View Solution
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
 View Solution
View SolutionA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View SolutionA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View Solution

