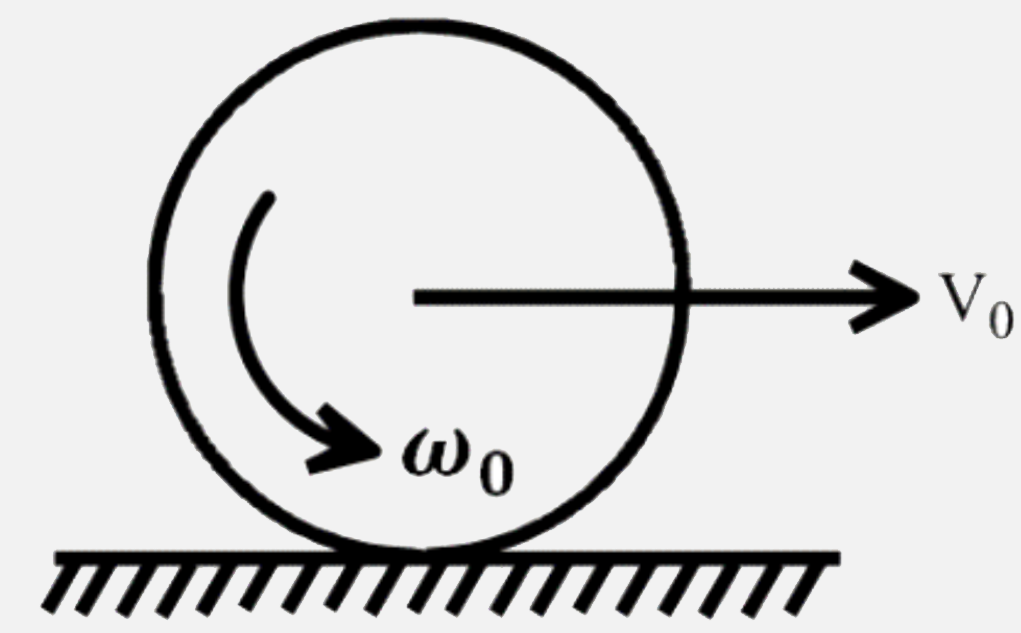
A disc of radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4 (at t=0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ. The sense of rotation and direction of its linear speed are shown in the figure. The disc returns to its initial point in time T=256kμgω0R. Find the value of k.

The correct Answer is:2548μgω0R
Step by step video & image solution for A disc of radius R is spun to an angular speed omega_(0) about its axis and then imparted a horizontal velocity of magnitude (omega_(0)R)/(4) (at t=0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is mu. The sense of rotation and direction of its linear speed are shown in the figure. The disc returns to its initial point in time T=(25)/(6k mug)omega_(0)R. Find the value of k. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A disc of the radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude (at t = 0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ . The sense of rotation and direction of its linear speed are shown in the figure . Choose the correct statement.
View Solution
A disc of radius R is spun to an angualr speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4. The coefficient of friction is μ. The sense of rotation and direction of linear velocity are shown in the figure. The disc will return to its initial position.
View Solution
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA metal disc of radius R rotates with an angular velcoity ω about an axis perpendiclar to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View Solution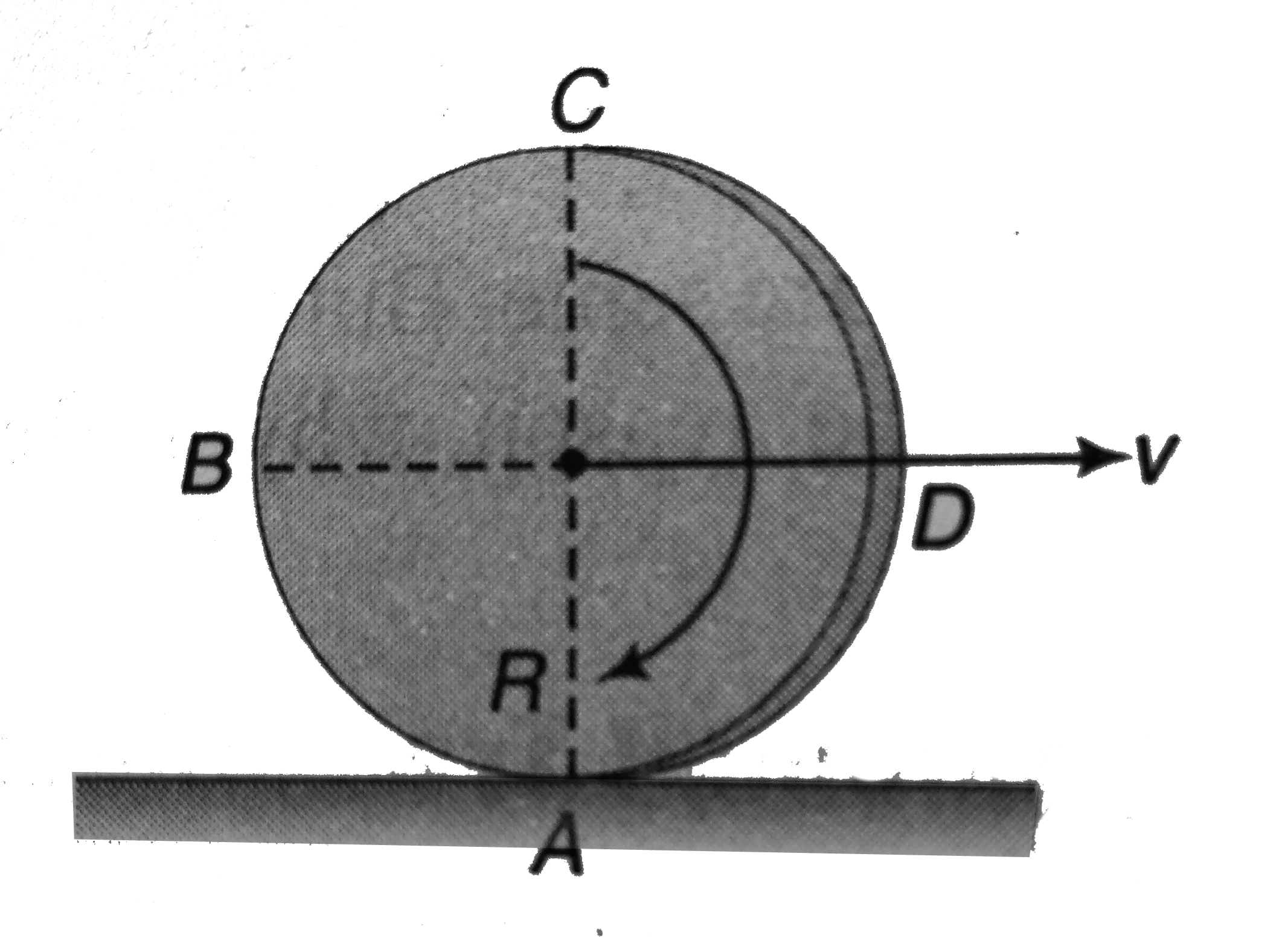
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View Solution
