In the figure shown in text, m1=m, m2=2m and initial distance between them is r0. Find velocities of the masses when separation between them becoms r02.
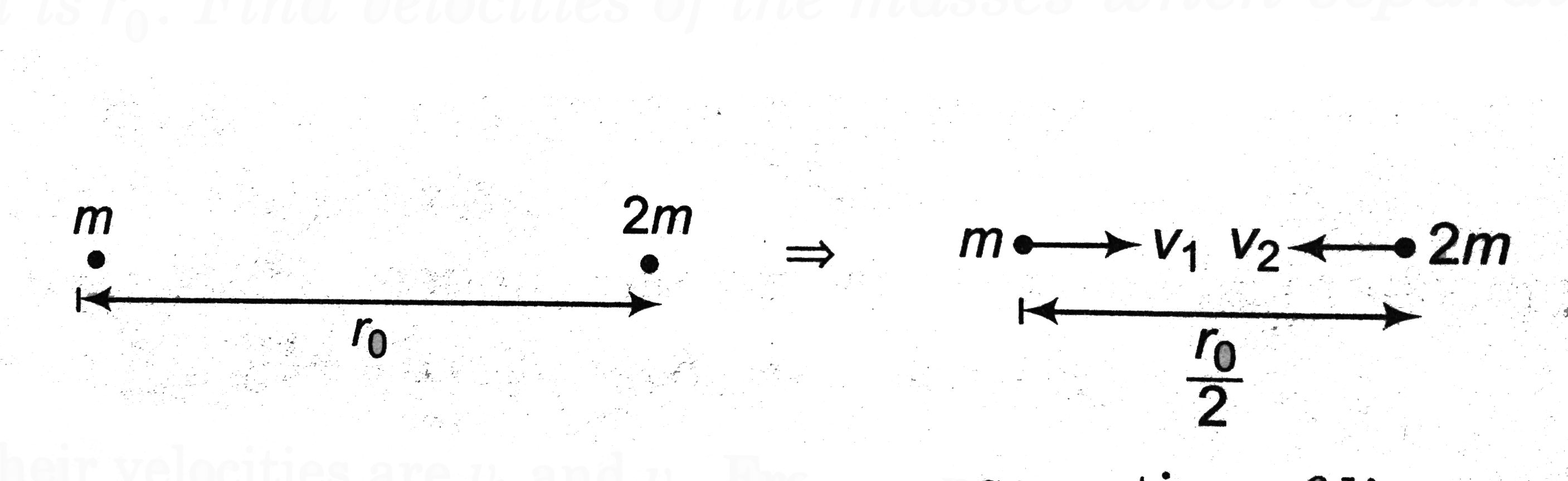
Let their velocites are υ1 andυ2. From conservation of linear momentum.
pi=pf
∴0=mυ1−2mυ2 ..(i)
From conservation of mechanical energy,
Ei=Ef
or Ki+Ui=KF+UF
or 0−G(m)(2m)r0=12mυ21+12×2m×υ22−G(m)(2m)(r2/2) ..(ii)
Solving Eqr.(i) and (ii), we get
υ1=2√2Gm3r0,υ2=√2Gm3r0
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.1
5 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
If the system shown in the figure is rotated in a horizontal circle with angular velocity ω . Find (g=10m/s2)
(a) the minimum value of ω to start relative motion between the two blocks.
(b) tension in the string connecting m1 and m2 when slipping just starts between the blocks
The coefficient of frition between the two masses is 0.5 and there is no friction between m2 and ground. The dimensions of the masses can be neglected. (Take R=0.5m,m1=2Kg,m2=1Kg)

View SolutionTwo points mass m and 2m are kept at a distance a. Find the speed of particles and their relative velocity of approach when separation becomes a/2.
View SolutionThe friction coefficient between the horizontal surface and each of the block shown in the figure is 0.2. The collision between the blocks is perfectly elastic. Find the separation between them when they come to rest. (Take g=10m/s2).

View SolutionTwo point particles of mass m and 2m are initially separated by a distance 4a. They are then released to become free to move. Find the velocities of both the particles when the distance between them reduces to a.
View SolutionTwo particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View SolutionTwo particles of masses m and M are initially at rest at an infinite distance apart. They move towards each other and gain speeds due to gravitational attraction. Find their speeds when the separation between the masses becomes equal to d.
View SolutionAssertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2
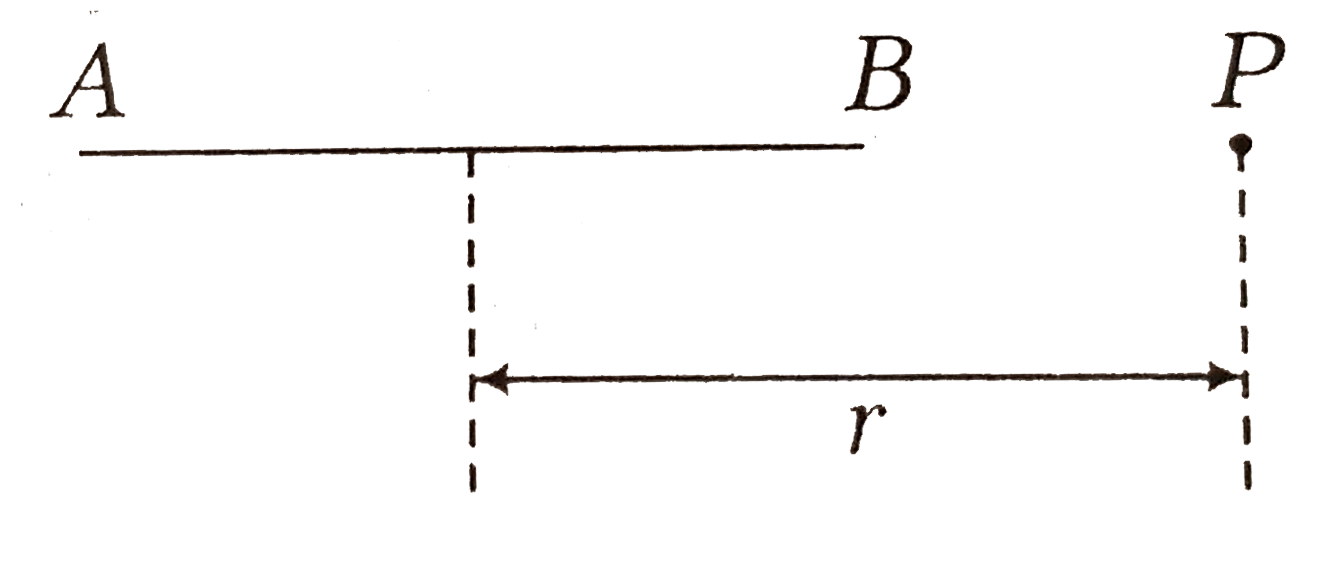
Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.
View SolutionPolice is chasing the thief 50 m ahead.In 10 s distance between them reduces by 6m. What is distance between them is 25 s?
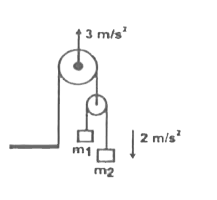
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
View SolutionTwo blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is

View Solution