In the problem discussed in the text, find E−r expressions for inside and outside points.
To find the expressions for the gravitational field E inside and outside a solid sphere with a mass density that varies as ρ=ρ0r2, we will follow these steps:
Step 1: Determine the mass inside the sphere
We start by considering a small spherical shell of radius r and thickness dr. The volume dv of this shell is given by:
dv=4πr2dr
The mass dm of this shell can be expressed as:
dm=ρdv=ρ0r2(4πr2dr)=4πρ0r4dr
To find the total mass M inside the sphere of radius R, we integrate dm from 0 to R:
M=∫R0dm=∫R04πρ0r4dr
Calculating the integral:
M=4πρ0(r55)R0=4πρ0R55
Step 2: Gravitational field outside the sphere
For points outside the sphere (at a distance r from the center where r>R), the gravitational field E is given by:
E=GMr2
Substituting the expression for M:
E=G(4πρ0R55)r2
This simplifies to:
E=4πGρ0R55r2
Step 3: Gravitational field inside the sphere
For points inside the sphere (at a distance r from the center where r<R), we need to find the mass M′ enclosed within radius r:
M′=∫r0dm=∫r04πρ0r′4dr′
Calculating this integral:
M′=4πρ0(r′55)r0=4πρ0r55
Now, we can find the gravitational field E′ inside the sphere:
E′=GM′r2=G(4πρ0r55)r2
This simplifies to:
E′=4πGρ0r35
Final Expressions
Thus, the expressions for the gravitational field E are:
- Outside the sphere (r>R):
E=4πGρ0R55r2
- Inside the sphere (r<R):
E′=4πGρ0r35
We start by considering a small spherical shell of radius r and thickness dr. The volume dv of this shell is given by:
For points outside the sphere (at a distance r from the center where r>R), the gravitational field E is given by:
For points inside the sphere (at a distance r from the center where r<R), we need to find the mass M′ enclosed within radius r:
Thus, the expressions for the gravitational field E are:
E=4πGρ0R55r2
E′=4πGρ0r35
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.1
5 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
In the problem discussed in the text, find the values of E and V at p dua to the remaining mass.
View SolutionA uniformly charged disc of radius R with a total charge Q lies in the XY -plane. Find the electric field at a point at a point P, along the Z-a xis that passes through the centre of the discc perpendicular to its plane. Discuss the limit when R>>z.
Strategy : By treating the disc as a set of concentric uniformly charged rings, the problem could be solved by using the result obtained in example for ring. Consider a ring of radius of radius r' and thickness as shown in figure.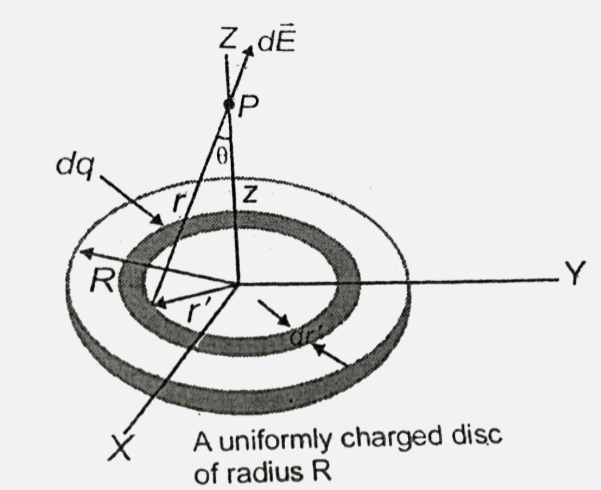
View SolutionA charged soap bobbe having surface charge density σ and radius r. If the pressure inside and outsides the soap bubble is the same, then the surface tension of the soap solution is
View SolutionFind the difference in excess pressure on the inside and outside of a rain drop, if its diameter changes from 1.003 cm to 1.002 cm by evaporation ? Surface tension of water is 72×10−3Nm−1.
View SolutionA cell of e.m.f. E and internal resistance r is used to send current to an external resistance R. Write expressions for (a) the total resistance of circuit, (b) the current drawn from the cell, (c) the p.d. across the cell, and (d) voltage drop inside the cell.
View SolutionA ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivities of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of the distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View Solution(a) Using Biot-Savart's law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show the magnetic field in the open space inside and exterior to the toroid is Zero.
View SolutionTwo point charges q1andq2 are located at →r1and→r2 respectively in an external electric field E. Obtain the expression for the total work done in assembling this configuration.
View SolutionUsing Gauss. theorem, obtain an expression for intensity of electric field .E. at a point which is at a distance r (r>R) from the centre Cof a thin spherical shell (of radius R) carrying charge.Q.
View Solution
