Assertion : If we plot potential versus x- coordinate graph along the x-axis, then field strength is zero where slope of graph is zero.
Reason : If potential is function of x- only then
Both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
Both Assertion and Reason are true but Reason is not the correct explantion of Assertion.
Assertion is true, but the Reason is false.
Assertion is false but the Reason is true.
The correct Answer is:D
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Understand the Assertion
The assertion states that if we plot the potential V versus the x-coordinate graph along the x-axis, then the electric field strength E is zero where the slope of the V−x graph is zero.
Step 2: Relate Electric Field and Potential
The electric field E is related to the electric potential V by the formula:
E=−dVdx
This means that the electric field is the negative rate of change of potential with respect to x. If the slope of the V−x graph is zero, then:
dVdx=0
This implies that:
E=−0=0
So, at points where the slope of the V−x graph is zero, the electric field strength E is indeed zero.
Step 3: Analyze the Reason
The reason states that if the potential is a function of x only, then:
E=−dVdx
This is a correct statement. If the potential depends solely on x, then the electric field can be defined as the negative gradient of the potential with respect to x.
Step 4: Conclusion
- The assertion is true because if the slope of the V−x graph is zero, the electric field strength is also zero.
- The reason is also true as it correctly describes the relationship between electric field and potential when potential is a function of x only.
Final Answer
Both the assertion and the reason are true. However, the assertion's implication about the electric field being zero solely based on the slope being zero needs to be carefully considered in a multi-dimensional context.
The assertion states that if we plot the potential V versus the x-coordinate graph along the x-axis, then the electric field strength E is zero where the slope of the V−x graph is zero.
The electric field E is related to the electric potential V by the formula:
E=−dVdx
This means that the electric field is the negative rate of change of potential with respect to x. If the slope of the V−x graph is zero, then:
dVdx=0
This implies that:
E=−0=0
So, at points where the slope of the V−x graph is zero, the electric field strength E is indeed zero.
The reason states that if the potential is a function of x only, then:
E=−dVdx
This is a correct statement. If the potential depends solely on x, then the electric field can be defined as the negative gradient of the potential with respect to x.
- The assertion is true because if the slope of the V−x graph is zero, the electric field strength is also zero.
- The reason is also true as it correctly describes the relationship between electric field and potential when potential is a function of x only.
Both the assertion and the reason are true. However, the assertion's implication about the electric field being zero solely based on the slope being zero needs to be carefully considered in a multi-dimensional context.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Single Correct27videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective19videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.75videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Assertion : The field strength at the centre of a ring is zero
Reason : At the centre of the ring, slope of V-r graph is zero.\View SolutionAssertion : If gravitational potential at some point is zero, then gravitational field strength at that point will also be zero.
Reason : Except at infinity gravitational potential due to a system of point masses at some finite distance can't be zero.View SolutionGravitational potential in x−y plan varies with x and y
coordinates as
V=x2y+2xy
Find gravitational field strength E.View SolutionAssertion: At a point electric potential is decreasing along x-axis at a rate of 10V/m. Therefore, x-component of electric field at this point should be 10V/m along x-axis.
Reason: Magnitude of Ex=∂V∂xView SolutionA graph is plotted with PV/T on y-axis and mass of the gas along x-axis for different gases. The graph is
View SolutionAssertion : x-t equation of a particle in SHM is given as :x=Acosωt
Reason : In the given equation the minimum potential energy is zero.View SolutionThe slope of the graph showing the variation of potential difference V on X-axis and current Y-axis gives conductor
View SolutionDetermine the electric field strength vector if the potential of this field depends on X, coordinates as V = 10 axy
View SolutionThe potential energy of a partical veries with distance x as shown in the graph.
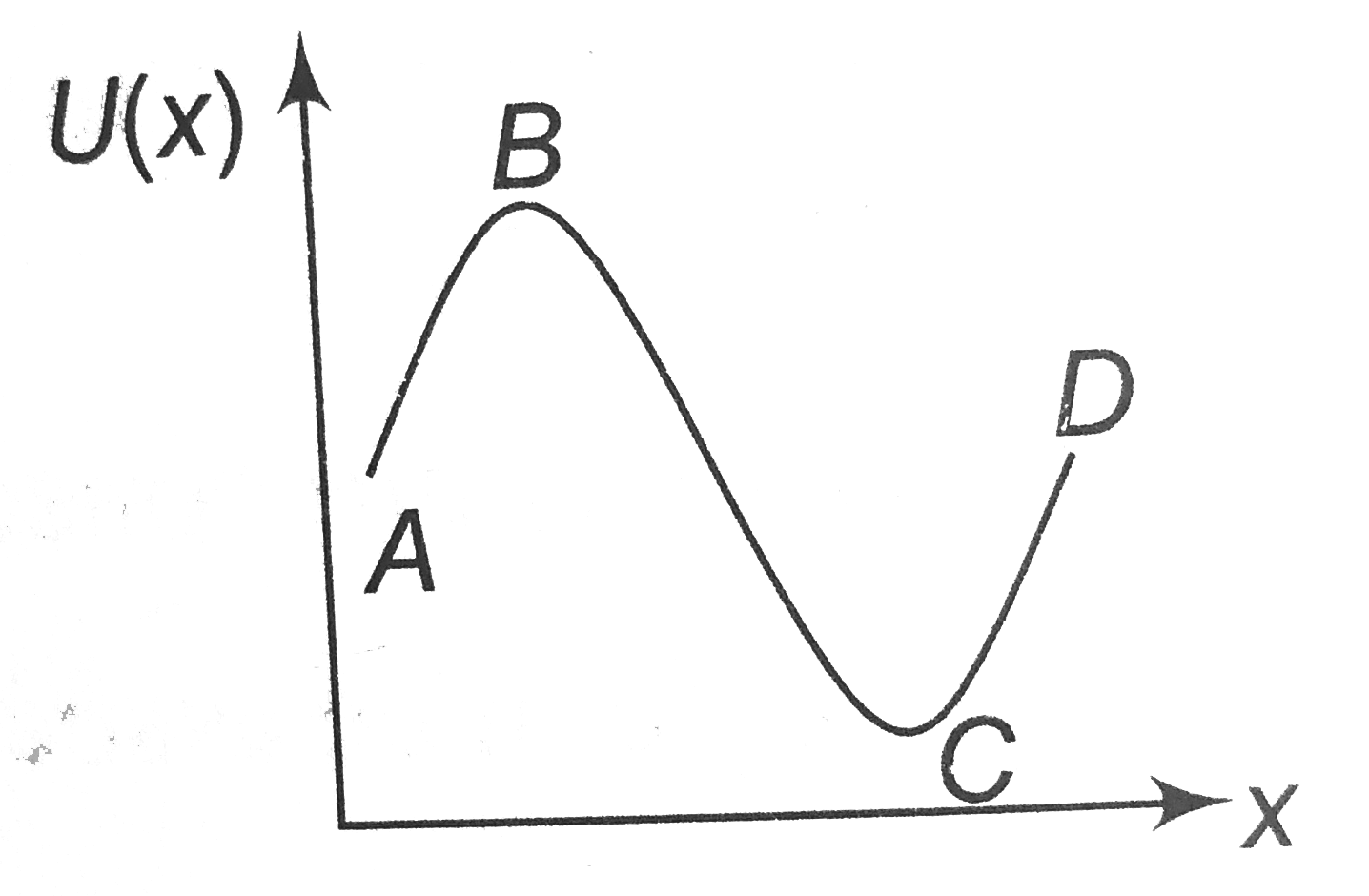
The force acting on the partical is zero atView SolutionAttempt this question on graph paper.
Reflect A and B in the x-axis to A' and B' respectively. Plot these points also on the same graph paper.View Solution

